Big Ideas, Goals and Details
In this article, I’d like to share some experiences and tips about teaching quadratic equations to Algebra 1 students. Use these ideas to modify your existing lessons or create something new on your own. I’ll lay everything out, step-by-step for you. If you’d like to try my lesson, you can find the information to do so at the bottom of the page.
We will see applications of two cool “teacher-tricks.”
- Setting the stage for the entire lesson by discussing a student’s question.
- Creating tension that is gradually resolved through the exploration of the lesson.
In the first exposure to quadratic equations, students got a little exposure to the parts of a parabola through graphing quadratics with t-charts. However, the training wheels were on! The t-charts gave students the x-coordinates of the intercepts and vertex, which was perfect for what they needed at the time.
It’s a great practice to set a lesson around a question phrased in “kid-speak.” One thing kids often wonder is, “Why do quadratics make parabolas?” That’s what this lesson is all about.
Goals and Questions
In kid-speak, students will answer the following questions.
- What is a parabola?
- What is a quadratic?
- How does a quadratic make a parabola?
To begin, start with a question like a kid would ask … for me, I chose, “Why do quadratic make parabolas?”
If you’d like to see a video lesson of what’s discussed here, click on the video to the right.
The Hook
Every good story, song, commercial, … you name it, has a hook. The kid’s question might be enough of a hook, but some added tension can make it so much stronger.
But, how do you create tension from a kid’s question in a math class? Controversy, of course!
I took the question and asked Chat GPT. I took a screen recording of the whole thing and posted it in my PowerPoint. In the guided notes I created for the lesson, which you can see to the left, students record what Chat GPT said, and then we explore the statements for accuracy and completeness throughout the lesson.
The controversy is that Chat GPT does a pretty poor job handling the question. In explaining why, students learn the objectives of the lesson! How cool is that?

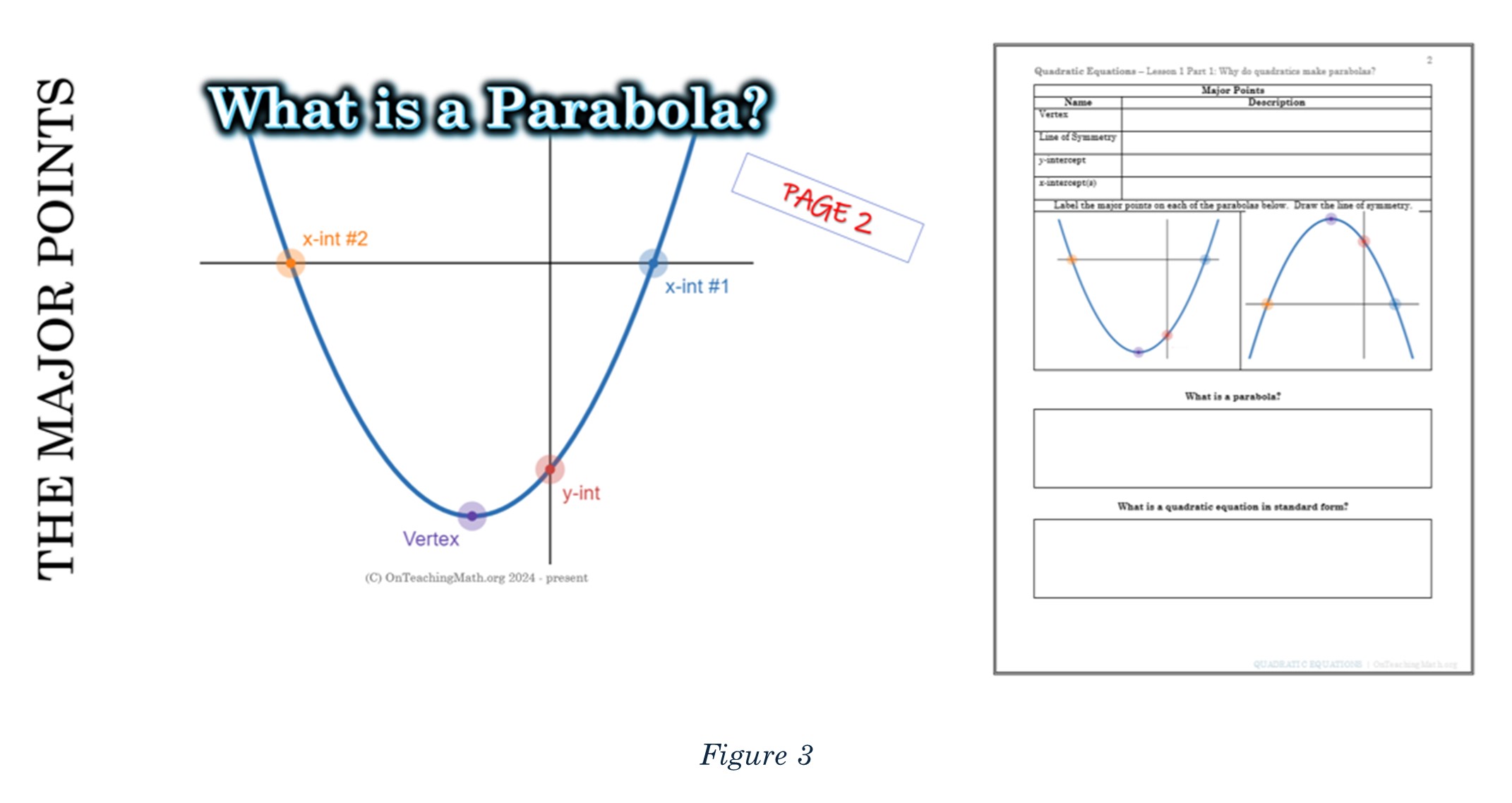
Claim #1 from Chat GPT: Of course, controversy is not required, but it helps grab attention. This is a good hook because it gets us through two of the questions to be answered. In Figure 2, I showed students the features of a parabola by comparing parabolas to the letter U and the letter V.
This was very effective and my students were creating the best parabolas I’ve seen from students just starting out in my career. I think the idea that they were doing something that AI misrepresented thrilled them a bit.

Consider adding a little animation of a parabola, like the one shown here. I made this in Geogebra using the tracing function. If you’d like to use this video and paste it into your own lesson, you can download it here.
Claim #2 from Chat GPT was solid. The direction of the parabola is determined by the sign of the leading coefficient, a. To drive this home, consider showing them a pair of almost identical equations in desmos. Get them to notice the difference in the equations before showing the graphs. Click one on and then the other and use this to promote conversation about the leading coefficient and the direction of the parabola.
To help them record their learning, give them a chance to sketch a parabola opening up, with a GIANT label that states a > 0, and another parabola opening down with a GIANT label that says a < 0.
Stuff Chat GPT Missed
Of course, if pressed, the AI would have given much better responses, but inaccurate and incomplete information served the purpose here.
For these lessons I like using guided notes. There is so much information to absorb that it’s easy for even the diligent students to get lost.
If you do this, consider posting in the lesson when it’s time to change the page. As you can see in Figure 4, the PowerPoint shows students they’re going to change the page, and the images are the same … yet the notes are missing a lot of information.
By setting things up this way, teaching can still stay organic, and conversational. However, if students need a bit of pressure and more structure because … they’re freshmen and that’s how it goes, then the guided notes can do that, too! But, the structure ahead of time really allows flexibility for you, while giving students the support they need.
This is where we dive into what Chat GPT left out. In the previous lesson, students learned what the vertex and intercepts were. So, this might be a good spot to give kids a few minutes to practice what they learned before, and maybe use their notes as reference.
This is a good time to strike home the idea of the vertex, how it is the minimum or the maximum, depending on the direction, and how the line of symmetry passes through it vertically. Depending on how solid students are with the parts of the parabola, this is a great time to stretch what they know, or just reinforce, depending on their needs.
This is exactly why a lesson does not teach itself. The teacher has to make decisions about what students need in real time!
So, What is a Quadratic?

Students will have heard this a few times by now, for sure. Still, they might recite the words, but will not truly understand.
Share with them a variety of ways that quadratic functions can appear, in both standard and vertex form. There’s no need to dive into vertex form yet, but exposure before the depth is a great practice. In Figure 4, you can a screen capture from the middle of this exploration. Students will be discussing what the coefficients are, when they’re equal to one, or zero, and how to read them from the equation.
For me, I’ve done this a few times at this point with students, especially when they were learning to factor, but still, new skills need reinforcement.
Finishing Up!
To this point, students will know the features of the parabola, both visually, and analytically. They’ll understand the smooth and continuous nature of the shape and can draw one. They can also find the vertex and intercepts (when a parabola is graphed).
It’s time to bring it home and tease out a tricky idea. Quadratic equations make parabolas because of the nature of the input being squared.
Students might not get it like will be said in the following sentence, but they should have a sense of this. A quadratic equation makes a parabola because as the inputs grow farther from the line of symmetry in either x-direction, the y-values grow at the same rate. In other words, “x-squared equals negative x-squared.”
A great way to tease this out is with a few extensive t-charts and detailed graphs. Have students observe, through your guided questions, the following things.
- Horizontal pairs of points are equal distance from the line of symmetry.
- A horizontal pair is the same vertical distance from the vertex.
During this exploration, it is a great time to tell students HOW they know if a point is an intercept or the vertex. Another great advantage of guided notes is that these ideas are recorded graphically and in written language! An example of how I structure these can be seen in Figure 5.

Now the Big Question for Teachers … What to Have Students Do With What’s Been Learned?
To me, quality practice is one of our biggest responsibilities and challenges. If it’s too easy, then it’s busy work. If the work is too difficult, then students just cheat or give up! They experience frustration instead of the success which energizes all of us who are successful when we get something right in math class.
Another component to useful practice is periodically revisiting old skills, especially those that are about to make a cameo appearance in upcoming lessons. Here, the future star will be factoring!
For this lesson, I give students four quadratic equations to graph from t-charts. Like last time, I chose appropriate x-coordinates that provided students with the intercepts and vertex. Students are expected to label each point, and name each of the coordinates as x-intercept, y-intercept, or vertex.
Then, I provided students with 5 fairly easy factoring questions, and then two linear equations to graph. With the linear equations, they had to find the intercepts and slope.
Resources
Please use the ideas, concepts, and practices described here in your existing lessons! After all, lessons don’t teach themselves, teachers do.
What makes a lesson good, or not, is the execution. That starts with cooperative students! Of course, that’s a massive topic that we’ll avoid for now except to say, that good relationships with students and a well executed lesson can help!
If, however, you’re starting from scratch and would like to use the resources I have created, you can do so with the links here.