To those of you returning, welcome back! I’m very glad you’re here. For those of you that are new, welcome. Every week, I pick a challenging and interesting math problem to share with you in this blog.
Why people do math for fun is a mystery to those who don’t enjoy math, but it is relaxing and challenging at the same time, like a good workout can be. Strangely enough, a student of mine is writing an extended essay for his International Baccalaureate program and his topic is about the meditative effects of doing math for fun.
This week’s problem was fantastic, it brought me a lot of joy. I hope you find something similar in it.
As always, I’ll share the details of the problem with you, then offer three clues to get you kick-started should you get stuck. Then, I’ll dive into my solution.

Figure 1 shows the situation. Our job is to find the area of the region shaded in red. The details are as follows.
A semicircle contains two smaller circles that share a common point on the diameter of the semicircle. There are two chords, each tangent to one of the smaller circles. One chord has a length of 3 units, the other is 5 units. That’s it!
Clues
Clue #1: Draw a pictogram formula showing what shapes make the composite shape that is shaded. Then, see if you can apply some formulas and identify what piece of information that is required to find the area.
Clue #2: Is there a way to express the information you seek in terms of information provided by the problem?
Clue #3: If you construct a radius of the semicircle perpendicular to the diameter that’s tangent to the small circles, it will bisect the chords.
Solution
Video
Let’s start with the formula. The semicircle and chords will provide us with the information we need but aren’t part of the formula of the red-shaded area. We will set those aside for now.
The shaded area is made up of two things, the circles. If the larger circle is solid red, and we subtract the smaller circle, we end up with the red-shaded region. See Figure 2 for a demonstration of this.

To find the area of the red-shaded region, we will take the difference of the two circles. If we call the large circle’s radius R and the smaller circle’s radius, r, we will get the following.
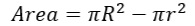
Time for my favorite oxymoron, a pretty ugly. What’s coming is pretty ugly, but is not very complicated. In short, we will create two right triangles from the center of the semicircle. The radius of each will be from that center to where the edge of a chord intersects the circle.
In Figure 3 you will see this construction. Since the hypotenuse of each circle is the radius, they are equal. The chords are bisected by the radius because the chords are both parallel to the base (diameter) of the semicircle. This gives us right triangle ABE and ACD. Notice that side AE is the diameter of the smaller circle (r), while AD is the diameter of the of the larger circle, (R).

It would make sense to use the Pythagorean Theorem to create some equations with R and r, so let’s do that now.
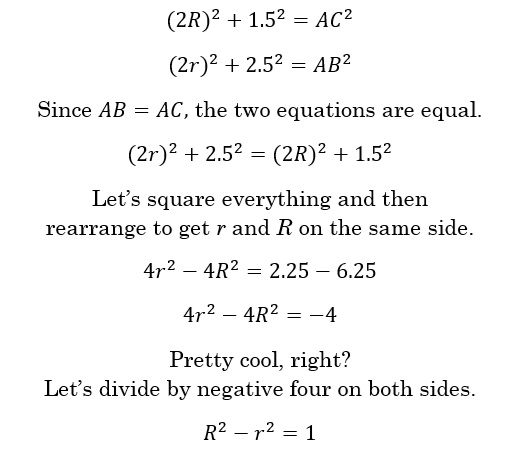
Now is a great time to bring back our formula for the area of the region shaded in red. Notice that the result of the Pythagorean Theorem is almost the same. It’s just missing a pi. So, we will multiply both sides by pi.
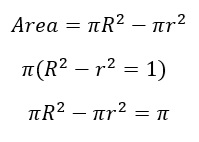
This tells us that the area of the red region is just pi! That’s pretty awesome! Do you see why the title is “I s-pi Something Red”?
Wrap Up
Another pi problem down! I’m a sucker for these things, I guess.
If you’re a math teacher and would like to use this, or other problems like it, in your classroom, the button below will allow you to download the PowerPoint presentation I used to make the video and create the images seen in this article.
