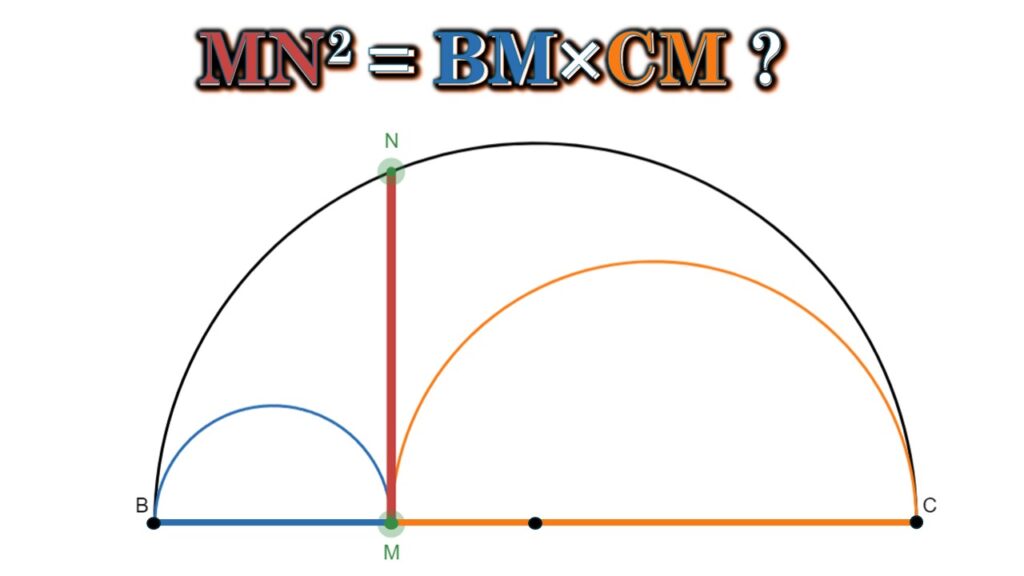
Welcome. For those of you returning, I’m glad you’re here. You’ll likely recognize the diagram above. For those that are new, welcome, I’m glad you’re here!
This week’s problem will be a bit different than normal problems. Last week we explored a cool little problem that had an answer of pi. It’s a surprising result and was a lot of fun. This week, we are going to explore and generalize some parts of last week’s shape.
Last week’s problem featured a large semicircle containing two smaller semicircles, and a line segment tangent to the two smaller semicircles. In Figure 1, below, the parts of this diagram are labeled appropriate for today’s exploration.
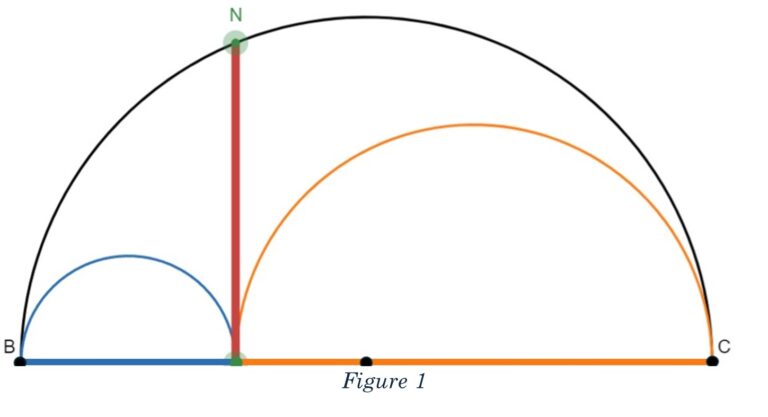
Quite a few people commented on the YouTube video asking if the size of the semi-circles really mattered? In short, yes, they do. The answer is only pi when the length of MN is 2. But, what we’ll find is that there is a relationship between MN and BM and CM.
You might point out that BM + CM is the diameter of the larger circle, which is true. However, what we will show is that MN-squared is the same area as BM times CM. BM times CM is different than the radius of the biggest semicircles squared because BM and CM make a rectangle, except at the endpoints and when M bisects BC.
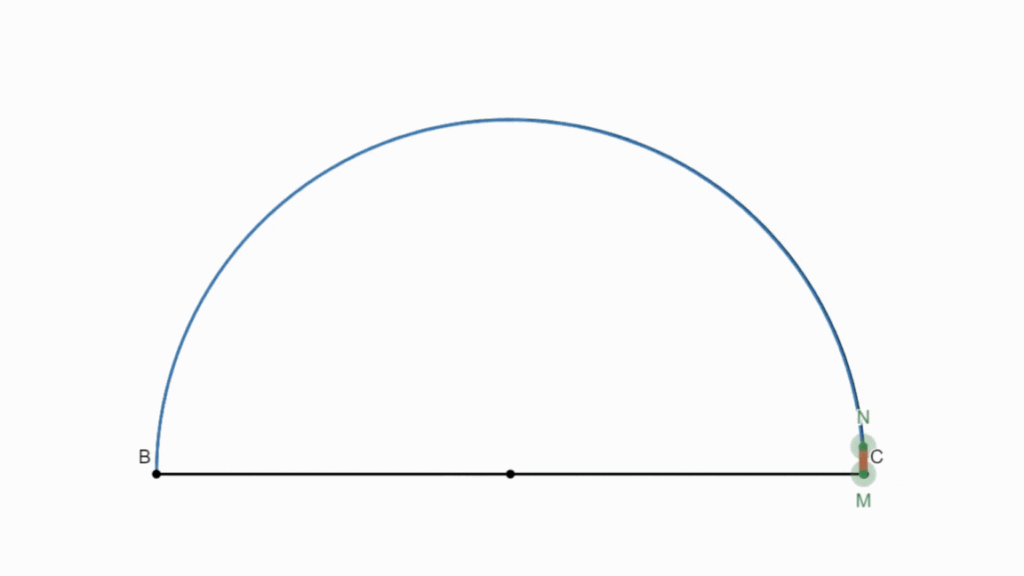
Let’s tackle two simple situations, then work on a generational solution.
If M is at the center of the large semicircle, then MN is the radius of that semicircle. BM and CM will also be the radius. So, MN-squared would be the same area as the product of BM and CM.
If M was at an end-point, B or C, then MN = 0. Either BM or CM would be 0 as well. 0-squared is the same as the product of zero and another number.
In both of these cases, MN – squared equals the product of BM and CM. But, what about the general case?
If you’d like to see a video of this solution, please click here.
For a visual representation of our general case, please see Figure 2.
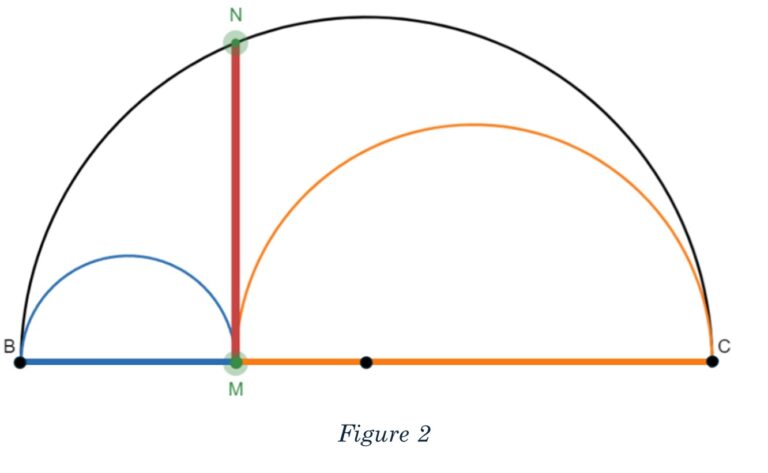
In our general case we have point M on the segment BC and point N on the edge of the largest semicircle. We have made the semicircle with diameter BM in blue and the semicircle with diameter CM in orange. We will keep the largest semicircle with diameter BC in black.
Let’s start by connecting N to B and then N to C, creating three right triangles. We know the triangle BNC is a right triangle because it is inscribed and lies on the diameter, making angle N ninety degrees. Since MN is perpendicular to BC, because MN is tangent to the smaller semicircles, triangle BMN and CMN are both right triangles as well, each having angle M being ninety degrees (Figure 3).
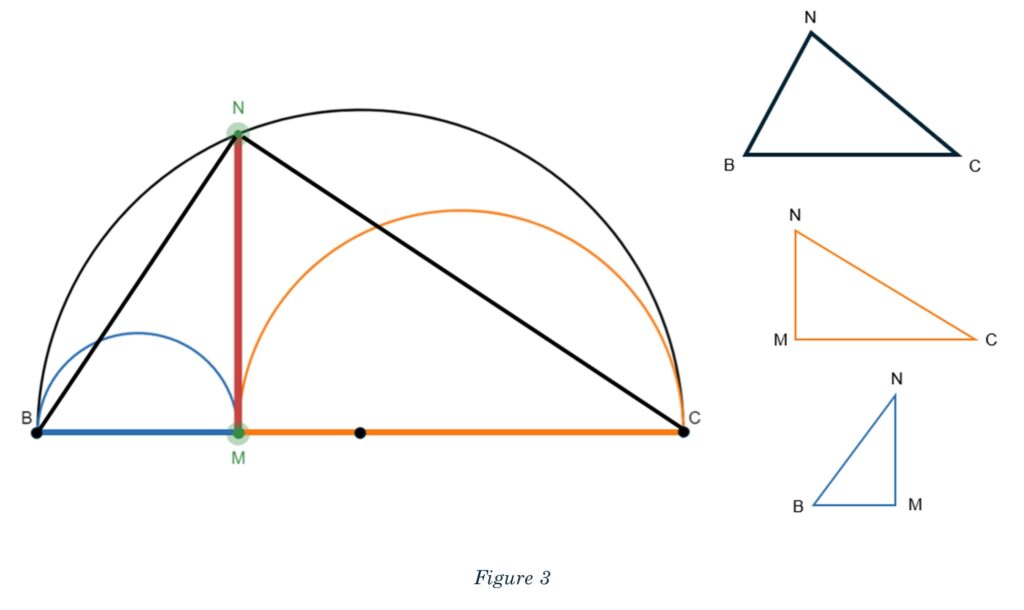
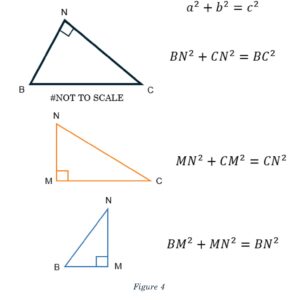
Now, let’s use the Pythagorean Theorem to write equations expressing a relationship between the sides of these triangles, which also include the diameters of the circles and the segment MN. Perhaps we can find some substitution of use! See Figure 4 for the work on these equations.
In our first equation, we have BC as the hypotenuse. BC = BM + CM. Let’s substitute that value in place of BC.
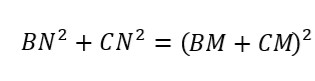
From our Pythagorean Theorem equations, we know what BN-squared and CN-squared equal, and we can square (BM + CM). BN-squared is BM-squared by MN-squared, and CN-squared is MN-squared plus CM-squared. Let’s do that work below.
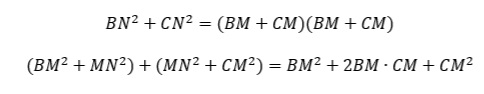
Both sides of the equation have a CM-squared and a BM-squared. We can subtract those terms from each side of the equation. This leaves us with MN-squared plus MN-squared, which is 2MN-squared.
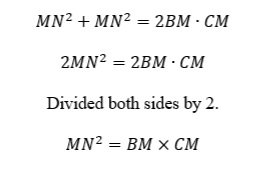
How cool is that?
The square of that chord is the same as the product of the lengths the chord separates the diameter into.
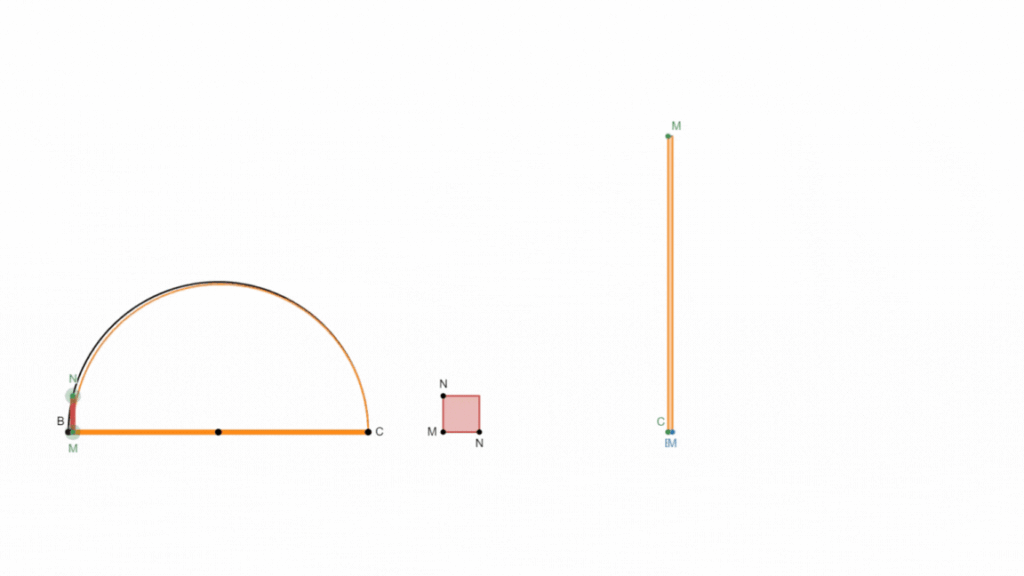
I’ll leave you with the GIF above showing the areas. They’re the same, at all values.
If you’d like to use anything found here in your classroom, please do so!
Here is the link for the DESMOS animation.
Here is the link for the PowerPoint that I used to make the images and video.
If you’re looking for some engaging, but easy to use resources in your math classes, please consider my TPT site.