For those of you that are returning, thank you! It makes me happy to know that others enjoy these weekly challenge problems. For those that are new, welcome! My name is Philip Brown and after two decades of teaching math, I got burned out. The fun of math was lost. In part, this blog is a way to practice the enjoyment of math. These problems are fun and intended to be tackled for the joy of doing math.
Like a hungry pug searching the kitchen floor, I search the internet for appropriate problems. When I find a good one, I save it on my phone. Usually on Monday or Tuesday afternoon I look through the problems I’ve collected and pick one. This week I found two that were very similar, which added a layer of excitement and accomplishment when I used the solution for one problem as a template for the other. That’s what we’ll uncover in this article.
As is the case with these questions, I’ll introduce the details, provide you with three clues, which you can certainly skip, but can return to if you get stuck, and then I’ll share my solution approach. If you have a better solution approach, I’d love to hear it. I’m no mathematician, I am always trying to learn and improve, so I would greatly appreciate hearing about different approaches.
Problem #1
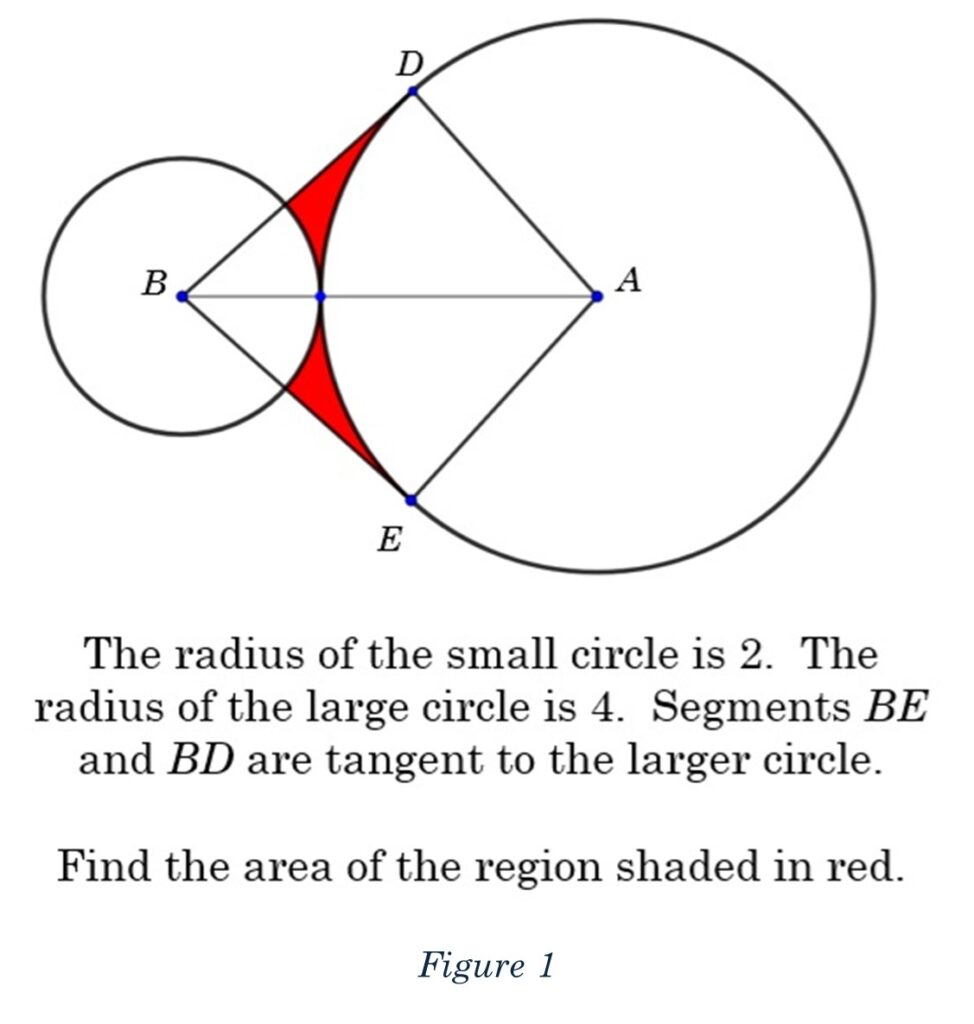
Two circles touch at one point. The smaller circle has a radius of two, the larger circle has a radius of 4. We will call them circle B and circle A, respectively.
As shown in Figure 1, segments BD and BE are both tangent to circle A. The tangent lines and edges of the circles create two small areas that are shaded in red. Our job is to find the area of the region shaded in red.
Problem #2
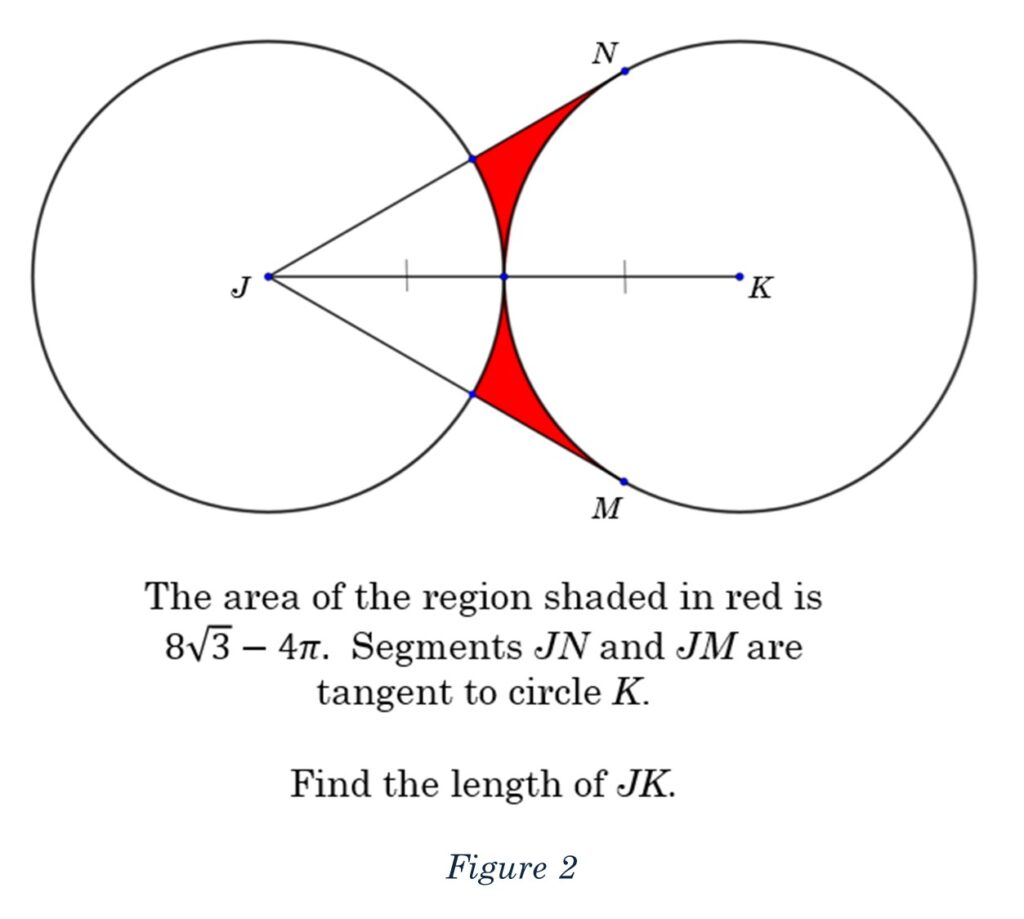
Problem #2
Two congruent circles touch at a point. Again, we have a pair of segments that start at one circle’s center and are tangent to the other circle, creating the regions shaded in red. This time, however, we are told that the area of the shaded region is Our job is to now find the length of the segment from one circle’s center to the other circle’s center. These details can be seen in Figure 2.
Clue #1
Picture – Good, Word – Bad. Draw a diagram of what shapes make up the shaded region.
Clue #2
Try some trig, cosine maybe.
Clue #3
For problem 2: Did you see how the parts of your answer from #1 came from various shapes that made up the shaded region?
Solutions
Let’s begin by tackling the first problem.
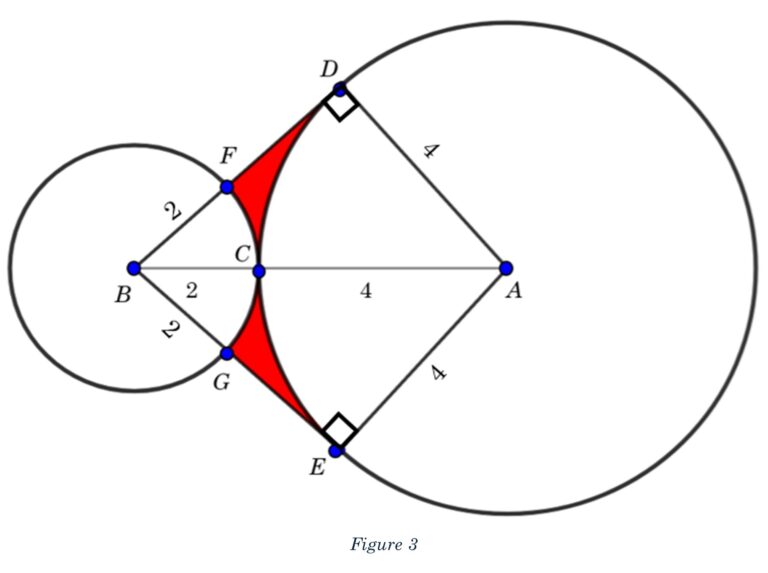
We are told that the segments BD and BE are tangent to circle A, making them perpendicular to the center. That creates a pair of nice right triangles, as shown in Figure 3.
The triangles are congruent, which might not be obvious, so let’s unpack that. If we look at triangle ABD, the hypotenuse, AB, is 6, and leg AD is 4. The same dimensions are true for triangle BAE. Since they’re both right triangles, we know the angles are also congruent. So, the triangles are congruent.
The region shaded red is bound within these two triangles, which form a kite. If we remove a sector from circle A, and another sector from circle B, from kite ABDE, what remains will be the region shaded in red.
I’ve found that it can be helpful to do the simple things carefully, like drawing a pictorial formula of what we’re after. See Figure 4 for the diagram of our current problem.
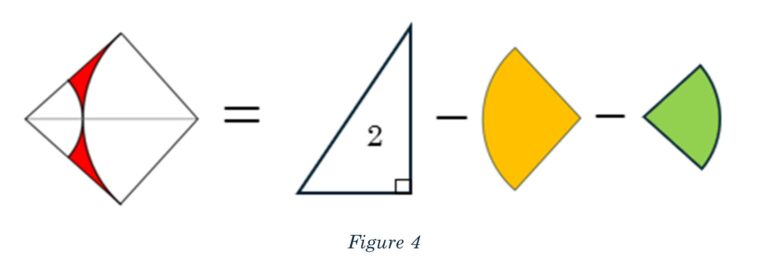
Now let’s tackle the parts, beginning with the triangle(s). We’ll figure out the area of one, then double it.
Triangle ADB is a right triangle with AD being the hypotenuse, length 6, and side AD being length 4. Let’s apply the Pythagorean Theorem to discover the other side so that we can calculate the area of the triangle.
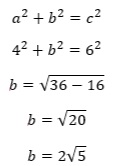
The area of a triangle is half of the base times the height. We will double that to account for both triangles, giving us the formula shown below.
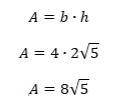
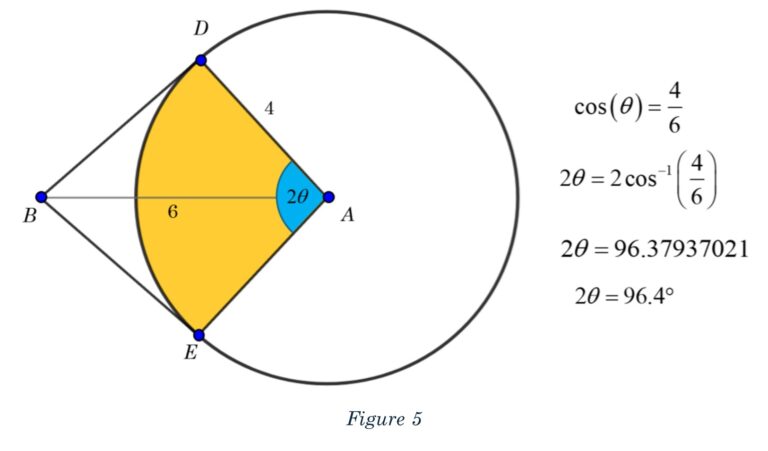
Let’s now tackle the area of the larger sector, ADE. The sector angle, DAE, is double the angle from the triangle DAB. Let’s start there since we can use right-triangle trigonometry.
We can use cosine to find the angle DAB. Since the adjacent side is 4 and the hypotenuse is 6, DAB is arccosine of 4/6.
Angle DAE is double that, so we can find which we will double to find angle DAE, which gives us 96.4°. Dang!
In Figure 6 you can see the diagram and working for this calculation.
A sector’s area is a portion of the area of the circle. We use the formula to find that the area of this sector is 4.28shown in Figure 6. We will keep things in terms of for now because the second problem expressions the values in those terms.
The angle for the other sector, BDE, is 180 – 96.4 = 83.6°.

Now that we have our pieces, let’s put them together.
That’s a pretty clean problem. It would be prettier is we didn’t have to round the area of the segments, but hey, not bad at all! Problem two is cleaner, and directly related. Let’s dive into that now and do so by using what we just learned.
The area of the region shaded red is “8root5 minutes 5.21pi.” The “8root5,” part was the area of the two triangles, or the kite. The 5.21 pi came from the sum of the sectors. That’s key information that will allow us to tackle problem #2! Let’s reintroduce it now.

Here we can see that the area of the shaded region is given in two parts, a term with a radical expression, “root 3,” and a term with pi. This is fantastic because we know the radical expression comes from the Pythagorean Theorem and the term with pi comes from the area of a sector.
We also know that the shaded region is constructed the same way! If we connect N to K, and also M to K, we will have another kite! The red area is the area of the kite with the two sectors removed.
Using our pictogram from before, we can label the information we’re given in the appropriate places, as shown in Figure 10.
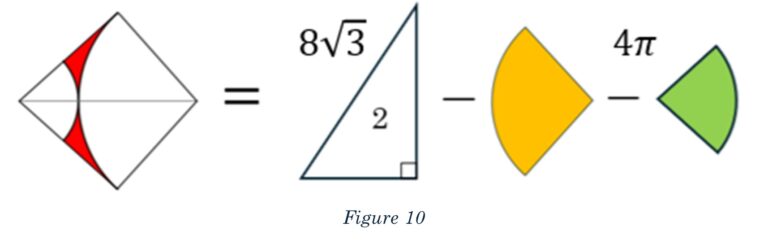
Let’s begin by writing an expression for the kite. To start we will consider each half of the kite, We will use the letters A through E again, and relabel our diagram. There’s not a mathematical reason for this, but those are the letters I used when I made up the diagrams.
In Figure 11 you can triangle ABD. You can see that BD is the radius of circle B and that the length AB is the hypotenuse of the triangle because segment AD is tangent to circle B, which makes AD perpendicular to the radius at the point of intersection.
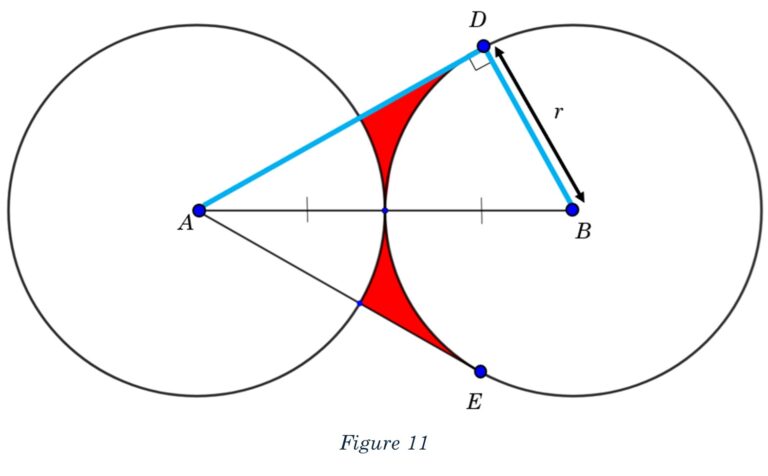
As was the case with problem #1, the area of the triangle is half of the base times the height. But, we have two identical triangles making up the region of the kite ABDE, so we will double the area of the triangle. The base is r, for the radius, and the height is AD. The area of the kite is rad, literally, r(AD).

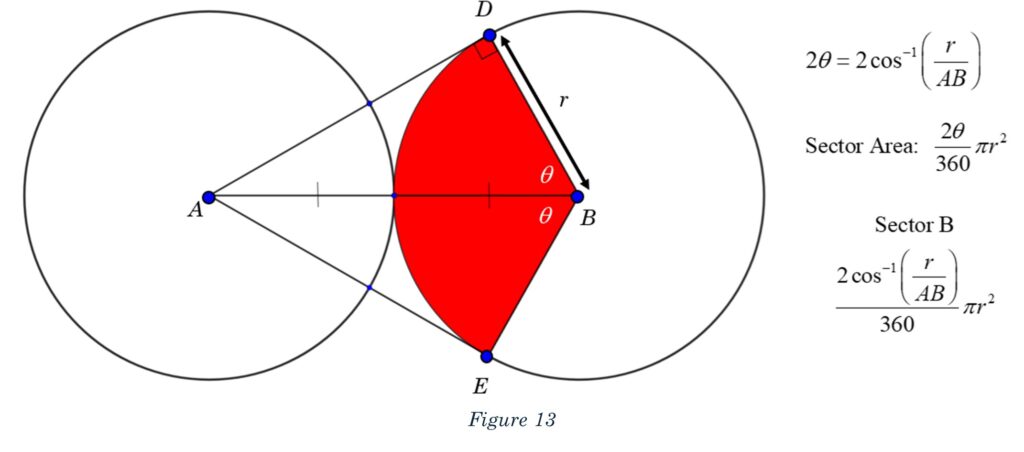
Even though the circles are congruent, the sector from each circle is different. Let’s start with the sector inside of circle B. We will use the right triangle to find the angle, then double it to find the angle of the sector. As we did earlier, we will use the formula for the area of a sector and to create our expression for sector B, shown in Figure 13.
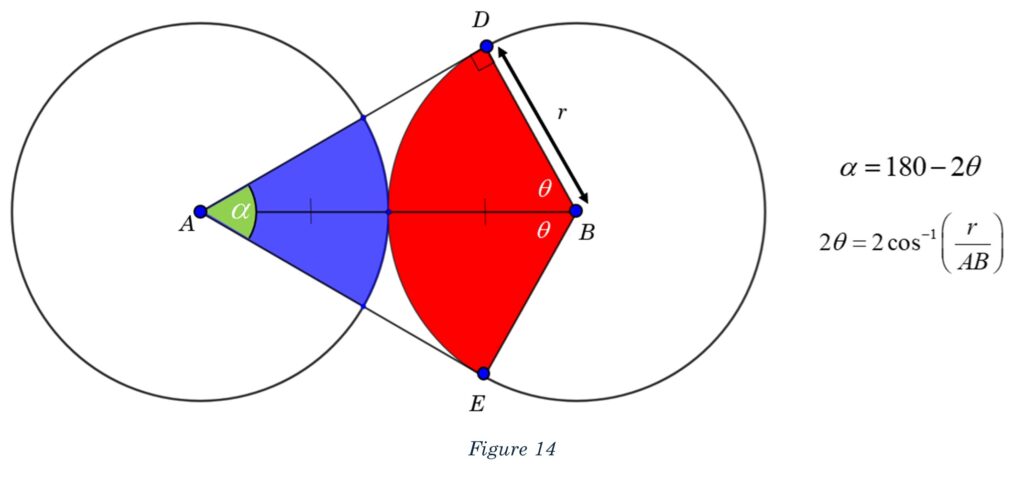
Angles DAE, which we need for sector A, is supplementary with angle DBE. You can see the calculators for angle DAE and its expression in Figure 14.
We will need to use some caution when manipulating the expression for the area of sector A, but it is not too difficult. There are just a lot of letters and expressions floating around. This work is shown in Figure 15.
We now have an expression for each sector. Now let’s do the algebra required to add these two together. The result gives us “half of pi times r-squared.”


Let’s put it all together now and see if we can find the distance between the two circles’ centers.
We are given the area is “8root3 minutes 4pi.” Remember, the “8root3,” term is from the area of the two triangles, or the kite. The 4pi comes from the sum of the sectors removed from the kite, leaving the red-shaded region.
We have expressions for the area where we found that the kite is r(AD), and the sum of the sectors is half of pi times r-squared. So we know that r(AD) = “8root3,” and that 4pi = half of pi times r-squared (Figure 17).

We can solve the equation with pi for the radius, and then substitute that value into the portion that describes the area of the kite.
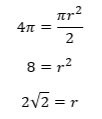
Now we will substitute this into the equation for the kite.
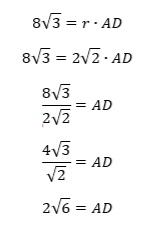
Let’s place these values on the diagram where will see that one more application of the good old Pythagorean Theorem will take it home for us, so to speak.
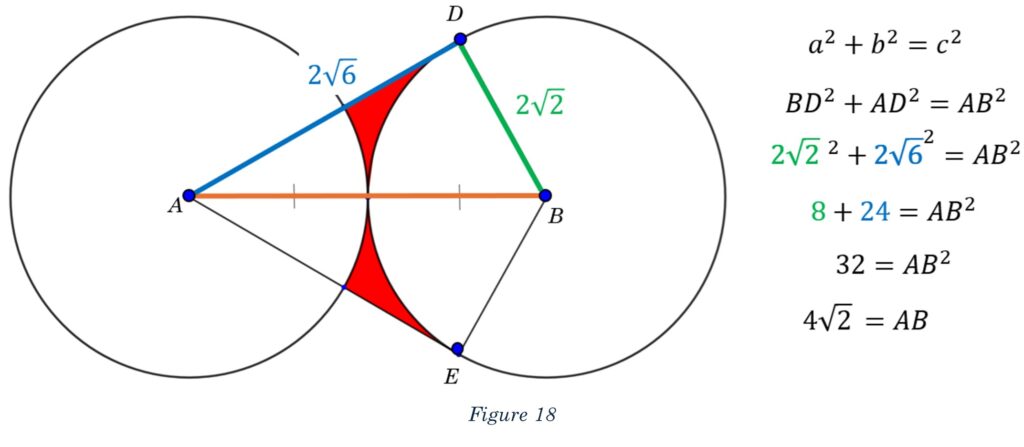
As shown in Figure 18, the distance connecting the centers of the two circles is “4root2,” which is a very nice answer!
Wrap-Up:
There was a simpler way to find the length of AB. I realized this when making the video for this problem. Did you discover it? If so, please let me know!
Other than that, how did you do? Did you have a nicer approach than mine, or something similar? I’d love to hear if you had something different.
Can you create your viral math problem now? For extra credit, try to make one, leave it in the comments and I’ll see if I can solve it. Maybe I’ll even write it up in a future article.
As always, if you’d like to use this problem in your classroom please use the buttons below.
Until next week, vaya con dios, as they say in the old movies!