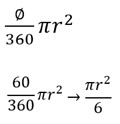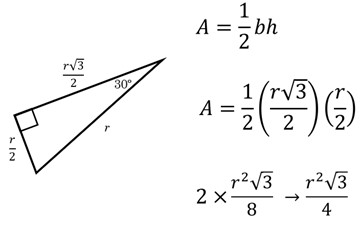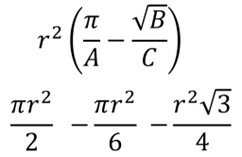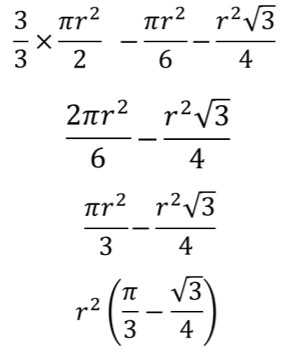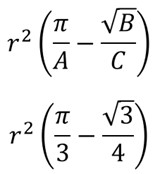This is a super cool problem, I love it! Here’s how we will tackle this one.
- Go over the details and demands of the problem.
- Offer three clues (which you can skip).
- Run through the solution.
- Celebrate!
The Set-Up
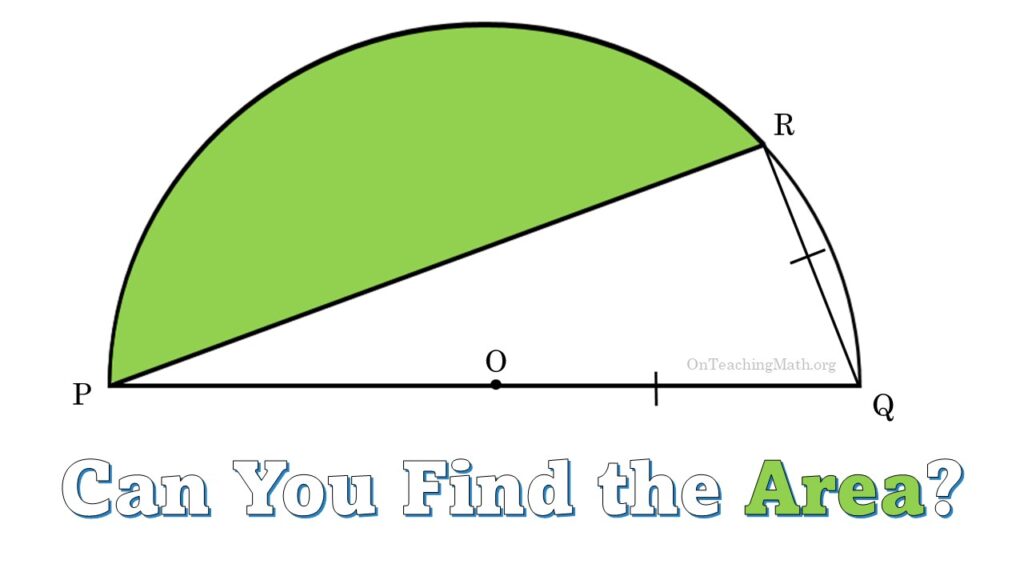
The diagram is not drawn to scale, but here’s what’s at play. There’s a semicircle with center O, and radius OQ. RQ is congruent to OQ. There’s a triangle inscribed in the semicircle with points PRQ. The region above the triangle is shaded in green and we need to find its area.

Clue #1
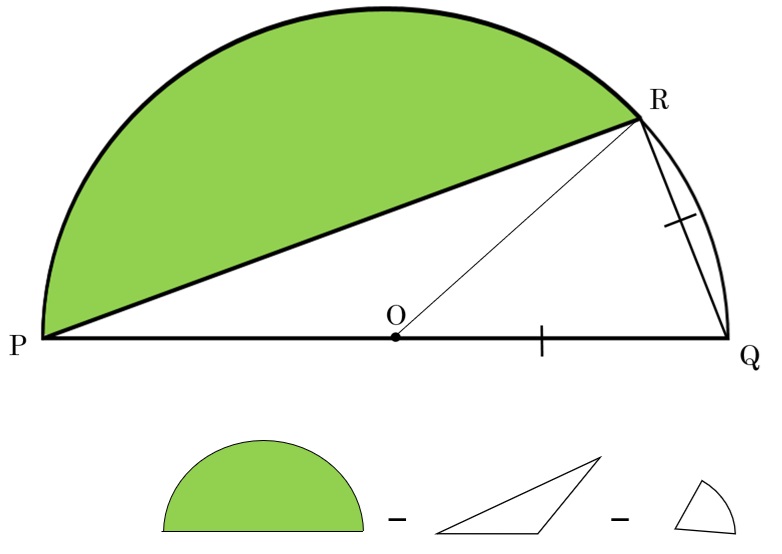
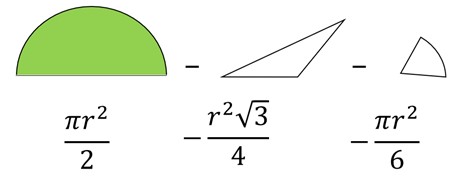
Can you write a formula, or draw a diagram, of the composite shape that separates the green region from the semicircle? If you started with the semicircle and then subtracted a sector and triangle POR (now shown in the original diagram), what would remain is the green region.
Clue #2
The sector ROQ has a central angle that is 60 degrees.
Clue #3
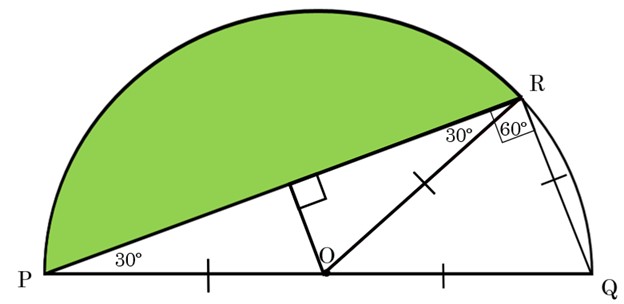
Triangle PRQ is a right triangle because it lies on the diameter and is inscribed. Triangle ROQ is equilateral. Armed with this information you can find the angles of triangle POR.
Solution
Now let’s tackle triangle POR.
Since ROQ is a 60-degree angle and PRQ is a 90-degree angle, angle PR0 is a 30-degree angle! That makes triangle POR an isosceles triangle! We can drop a perpendicular bisector giving us a nice 30-60-90 right triangle with the hypotenuse being the radius of the semicircle. How sweet is that? Really, I mean, come on! If only all of life’s problems were set up to be solved with such beautiful arrangements and discovery. This feels like a real-life Magnum PI episode!
I really hope you enjoyed this problem. I did!
If you’re a math teacher, I’d like to encourage you to use this in your classroom. I post a weekly math for fun problem. Students are not incentivized to work on them, just invited passively. Those that decide to tackle the problem do so for the fun of it, nothing more. I think it’s a great way to steal some fun and enjoyment of learning back from the tyrannical pressure of grades, GPA, and scholarship opportunities.
If you’d like to use this problem in your room, use the links below.
Until next time, this is Philip Brown, signing off!