For those of you returning, welcome back. An exciting problem is ahead, one that can be surprisingly slippery. For me, it felt like looking at the Pleiades constellation where it’s somehow clearer peripherally.
For those of you that are new, welcome. Every week we tackle a math problem for fun! There’s no other reason than to exercise the noodle tool and find a little entertainment that isn’t an infinite scroll of TikTok videos.

A few weeks ago, we worked on a problem with two inscribed semicircles whose diameters coincided with a larger semicircle and a chord of the large semicircle that was tangent to the smaller two. From that problem, we showed a general case where the product of the diameters of the semicircles was equal to the square of the chord, as shown in Figure 1. If you’d like to revisit that derivation, please click here.
This week’s problem has a circle inscribed in a square and another smaller circle inside the inscribed circle. A few dimensions are shown, and the task is to find the area of the square.

I found this problem (Figure 2), on a Facebook page, the author is Assel Lessa, which is a palindrome. If that’s the person’s actual name, well, that’s pretty much awesome! If it’s a pen name, that’s pretty cool, too! My fawning over the name aside, the problem is clever, as are most of the problems I’ve found posted by this person.
I believe there is only one piece of information that needs to be assumed. The segment of length six could be extended to intersect where the circles are tangent to the square on the opposite side. For example, there is a dotted line connecting the segments of length four. Another dotted line connecting the length of six to the opposite side would show that the segment is perpendicular to the square’s side. I don’t think that information is otherwise discoverable. To solve the question, it must be assumed as the intent of the author.
If you’d like to see the Geogebra file I created to capture this image, click here.
If you’d like to try the problem now, now is a great time to do so. Print the diagram, or sketch it, and get comfortable. Explore it a bit, you’ll likely stumble upon pieces of information that can be linked together to reveal the answer.
Solution
In the video, I shared two separate solutions. Here, I will unpack just one, the solution involving the property described at the beginning of the article.
The area of the square is the length AB-squared. AB is the same as the diameter of the inscribed circle. If we say the circle’s radius is R, then AB = 2R. If we can find R, we can double it, then square that product, and boom, we’re done!
Let’s begin by labeling a few of the clues on the diagram. In the diagram, you can see that the radius R is 6 + x, and is also 4 + y. These relationships are shown in Figure 3.
This is a pair of equations with 3 variables, so it cannot yet be solved. We need a third equation. That’s where the chord-diameter relationship comes into play.
In Figure 3, you can also see how we find the third equation, where the segments that create the diameter of the smaller circle, x, and R, have the same area as the chord length squared.

From here, there’s a little bit of Algebra and substitution. Let’s dive in.
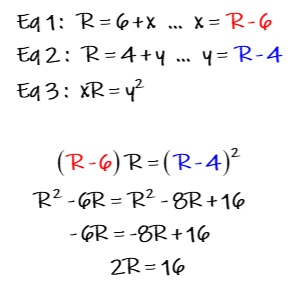
The area of the square is AB-squared, and of course AB = 2R. Since 2R = 16, the area of the square is 256 units.
Did you enjoy this problem? Let me know.
Do you have a different solution, maybe a cleaner one? If so, I’d love to see it!
Until next week, enjoy!
