For a student who just finished up linear equations and maybe a bit of distributing and combining like terms with polynomials, quadratic equations are quite the leap!
We will start small, with the foundational ideas, having students explore each along the way. As we introduce new concepts and procedures, we will tie them into the prior experiences of the students. We will continue this process until students have built a comprehensive and robust understanding of quadratic equations.
Ready to get started? Let’s give ’em MATH!
Before We Begin ...
Below are two reference sheets that are appropriate for students learning quadratic equations. Download these and distribute them to your students. Encourage their frequent use throughout the lessons by making them a required daily material, like a pencil and willingness to learn!
First Big Idea: Graphs are Pictures
The idea that a graph is a picture that tells the story of an equation might seem simple to a mathematician, but to someone just starting, that’s a massive intellectual leap of faith!
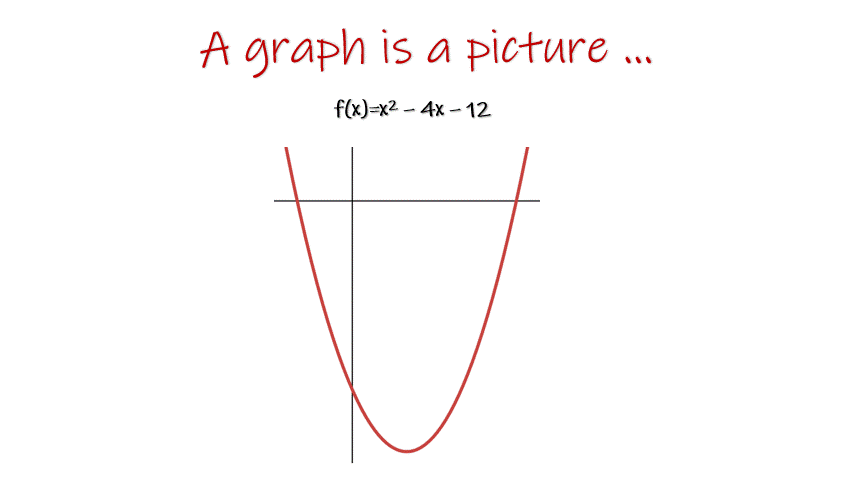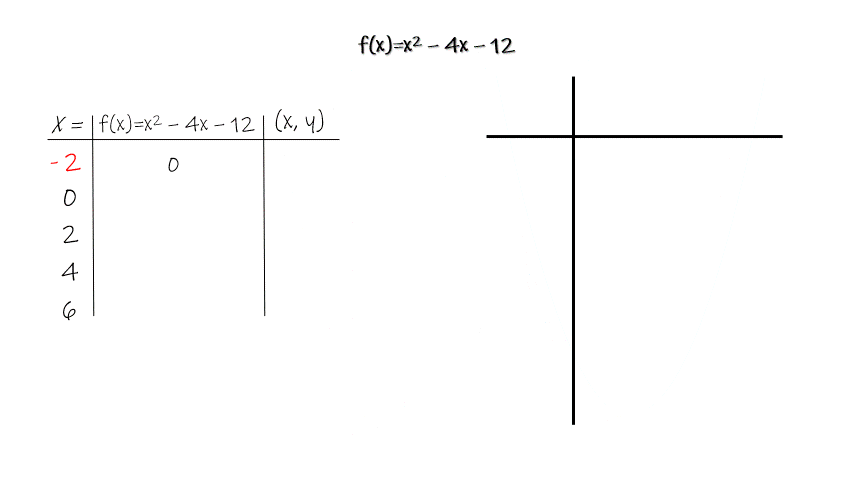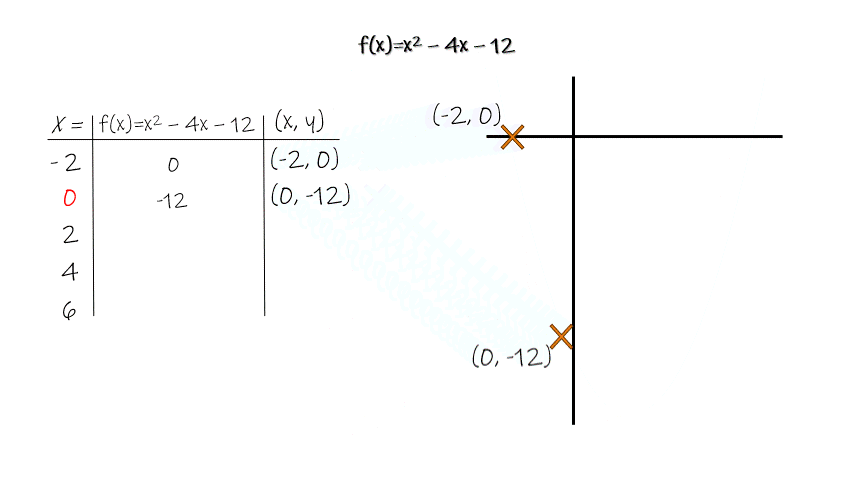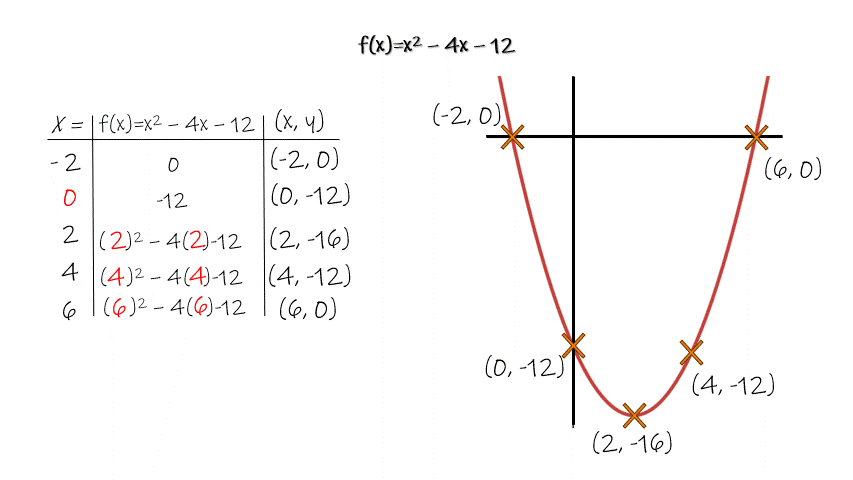
To help students develop this idea have them work with t-charts. Pick some “easy,” quadratic equations, both in standard and vertex form. Then, set up the t-chart for them by choosing the x-coordinates for the vertex, y-intercept, and x-intercepts.
You’ll likely be surprised to see how difficult this can be for students. There is good reason. Linear equations are far simpler than quadratic. Now students have an exponent and grouped numbers to navigate!
During this process, students will be learning the parts of a parabola, as well as how to read function notation (how to evaluate a function for a given input). Don’t worry about being too formal, all of the new concepts will be revisited throughout the unit!
Spending time early on developing basic skills and exploring the essential concepts is an investment that pays off.
Students will be armed with the experience and knowledge required to maneuver the difficult algebra that is ahead!
If you’d like to see, more specifically, how I tackle these first ideas and what tasks I give to students, the video posted here shows exactly that.
Before moving from one part to the next be sure to assess your students. That check-for-understanding is the only way to inform you and the students of their progress!
Here is a Google Forms assessment that I really like to use before moving on. Click on the icon to try it out.
If you’d like a copy of the quiz, click here.
Second Big Idea: All Quadratics Make Parabolas
... and what is a parabola anyway?
By now students will have graphed a few quadratic equations and plotted the vertex, y-intercept, and x-intercept(s). Every equation will have been quadratic, and every graph a parabola, and since you chose the x-coordinates, every parabola would have the vertex, y-intercept and x-intercept(s) marked with a specific coordiante.
This second big idea is about connecting those experiences with what a parabola is, what the key features and parts of parabolas are, and the fact that all quadratic equations make parabolas when graphed. The parabola tells the story of the quadratic equation!
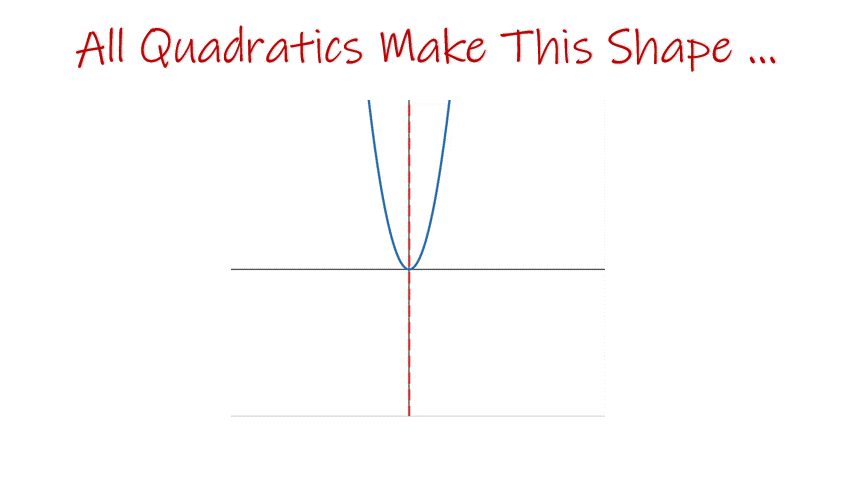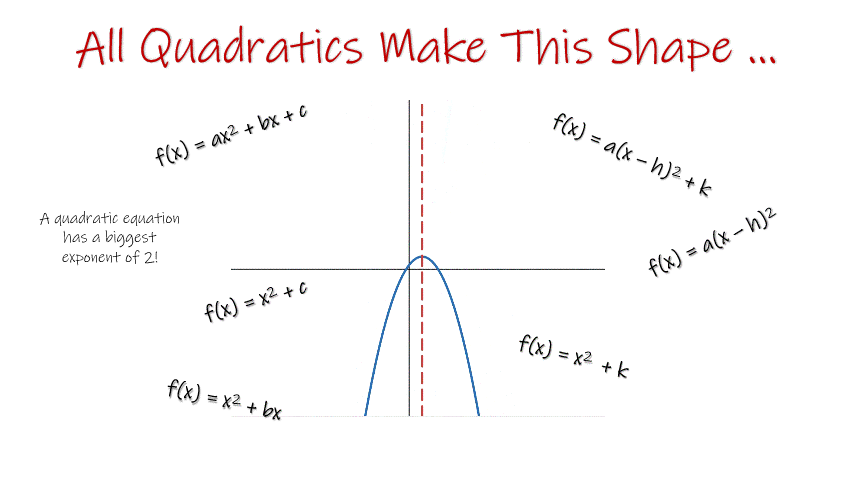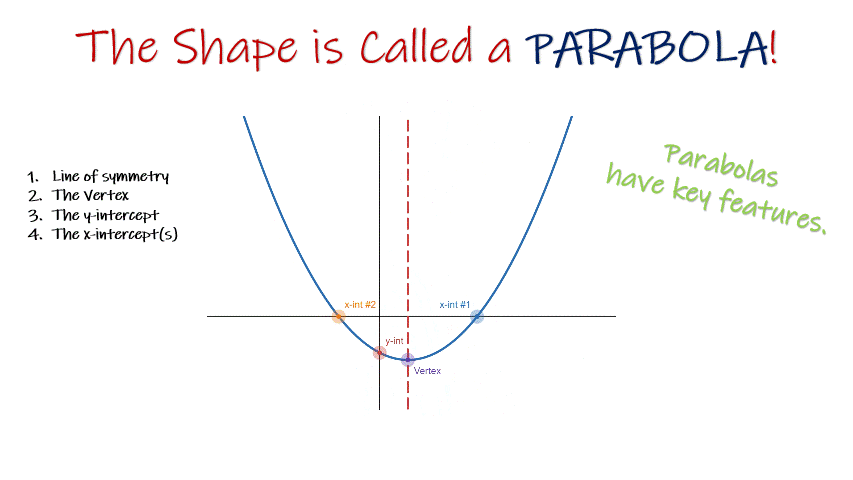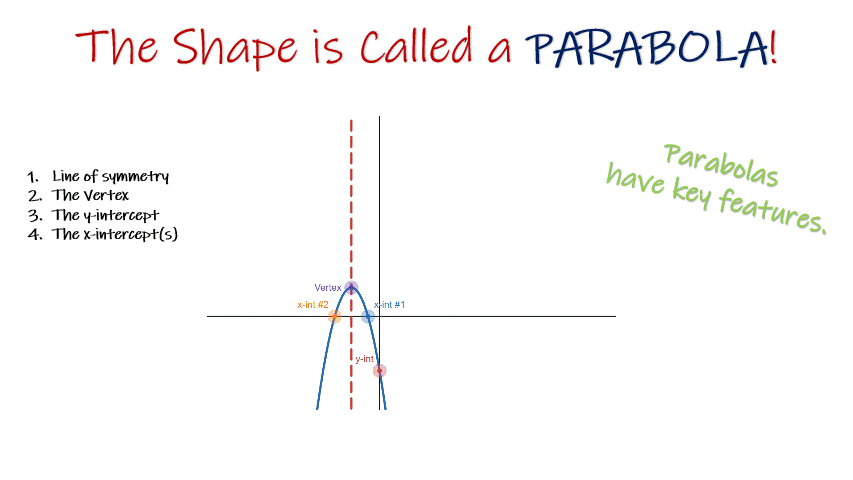
A great way to make this connection is to teach students how they know if a point is a vertex, an x-intercept, or a y-intercept. It’s also a great time to draw out a few key concepts through graphing.
- The leading coefficient determines the parabola’s direction.
- There is always a vertex and always a y-intercept.
- There could be 2, 1, or 0 x-intercepts.
Once again, before moving on have a formal assessment. The test is a chance for students to practice what they’ve learned. It’s also the only way for you and the students to know how things are going. This is crucial information for all parties.
To the right is an example of a Google Forms quiz I use at this point. Click on the icon to try the quiz yourself.
If you’d like to download a copy for your classes, please click here.
Third Big Idea: The Parts of a Parabola
... and how to find them.
The x-intercepts are the trickiest parts and require the most fluid understanding and mathematical abilities.
I treat them as the last part in this unit that introduces quadratic equations.
Now is when we begin to introduce some of the more difficult formulas and processes. Since still will understand what the formulas will produce, they’re much more willing to “play along.”
A little faith and willingness goes a long way. This is where the extra time spent earlier in the unit begins to pay off!
Students feel a lot more confident if they know that they can at least begin a process. So, start with the y-intercept, in both standard and vertex form. But, drive home the idea that the y-intercept is not just “c” because, but rather due to the fact that x = 0 for any y-intercept because it lies on the y-axis.
So starting with the y-intercept is a great way to build confidence.
Students learn by doing, however, a little structure in what they’re doing can go a long way.
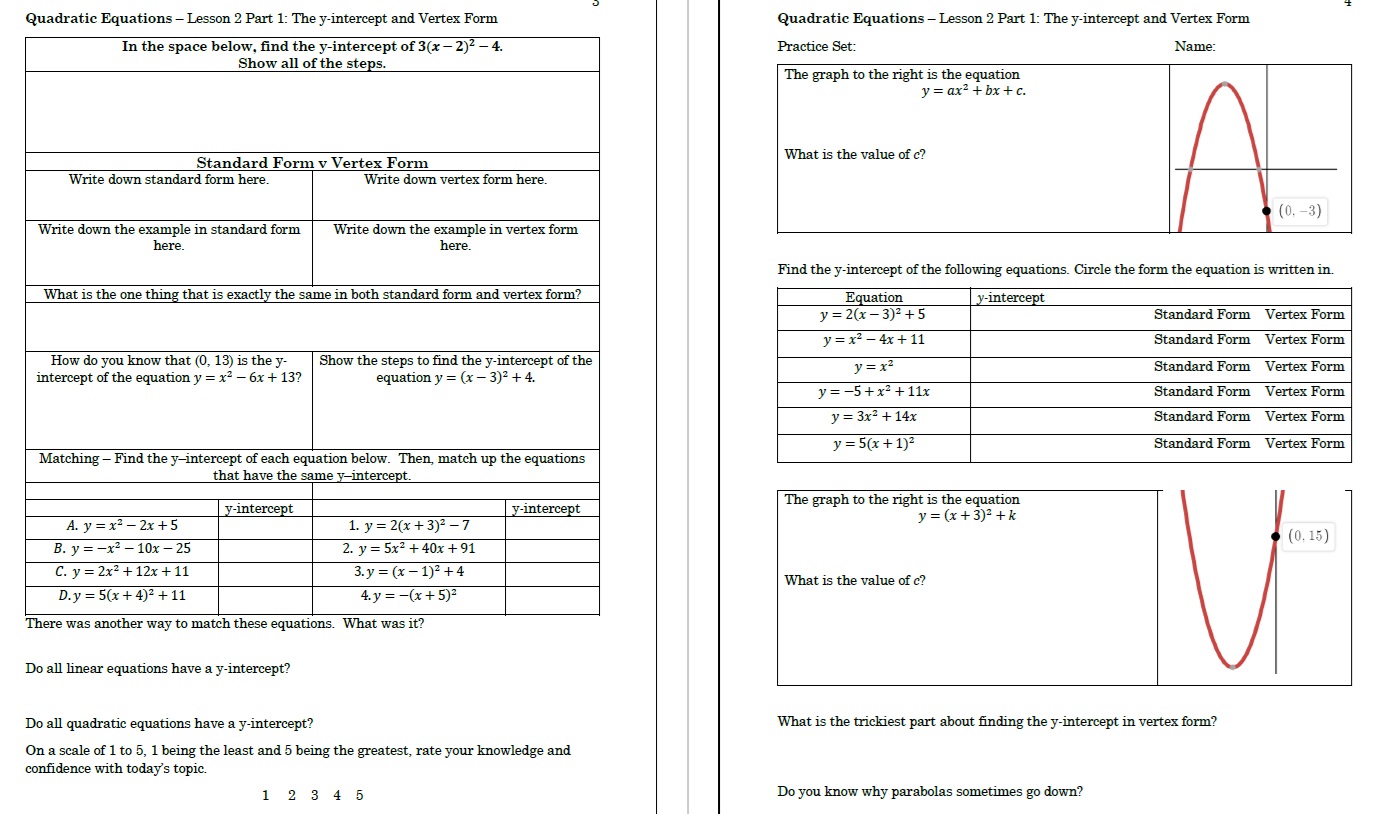
It’s a great idea to have them explore finding the vertex and y-intercept of quadratic equations with some structure. To the right you can see an example of how to structure the homework and lesson. The left-hand sheet is the end of the guided notes for the lesson, and the right-hand side is the beginning of the practice set.
Two things you should consider adding to your notes and practice are metacognitive questions where students evaluate their learning as well as periodic questioning related to, but not the focus of, that particular lesson.
You can see examples of these in the picture to the right. Click on it to zoom in.
If you’d like to see how I structure the lesson the y-intercept, please watch the video below.
The vertex is perhaps the most important part of a quadratic equation’s parabola. That is why it is something students need a lot of time and varied practice with.
Some step-by-step structured work, along with games, activities, group work, and so on, can really help students get the meaningful experience required to master finding the vertex and understanding what the vertex is and what it means.
Notes About the Vertex
Have students explore how the line of symmetry passes through the vertex vertically. Then, each arm of the parabola is a reflection across the line of symmetry.
Any horizontal pair of points is equal distance from the line of symmetry … especially the two solutions!
This is THE GROUNDWORK for the x-intercepts and has a strong Geometric connection.
Below you can see how I approach the concept of horizontal pairs being equidistant from the line of symmetry.
Last Idea: The x-intercepts
Finding x-intercepts can unravel a lot of content. That’s why quadratic equations are often introduced in an Algebra 1 class and then continued in an Algebra 2 class. If we chase the x-intercepts far enough we include completing the square and eventually we dive into complex numbers.
How deep you can go here depends on your students and how much time you have to devote to quadratic equations. At a minimum, I’d suggest that students know the following.
- There are either 2, or 1, or zero x-intercepts.
- Students can find x-intercepts by factoring.
- Students can find x-intercepts with the quadratic formula.
- BONUS: Students can use the M – D formula to find the x-intercepts.
With a high-achieving group, this is the time to introduce completing the square, which will be used to derive the quadratic formula. However, the focus of this block of lessons is to develop a foundational understanding of quadratic equations. It is better that students understand a few concepts well than to have a weak exposure to all of the concepts.
Teach Factoring to Find x-intercepts First
The key to teaching factoring is to tie in the idea that factor is “distributing backwards.”
When we factor we are rewriting an equation in small and simpler parts. Those parts can be examined and will reveal the x-intercepts as a result of zero-product property.
Below you can see a video lesson that shows one way to highlight this connection.
Now, of course the title of the video isn’t quite right, factoring doesn’t find x-intercepts, but it is exactly how many students pose the question when they’re learning how to find x-intercepts by factoring!
Second: Using Inverse Operations to Find x-intercepts ...
Students should be able to determine which method of finding x-intercepts is most appropriate. In other words, we cannot give them too many clues as to which process to apply for any given problem.
With this in mind, vary the types of problems students practice and the resources you pull from for practice sets.
While it is true that the quadratic formula always works, it’s not always the best option. It is a complicated formula that requires accurate manipulation of signed numbers, the order of operations, square roots, and reducing. Sometimes, there are much simpler ways and students need to be able to navigate which tools they have and when to use them!
Don’t get too laser-focused here.
The MD or PQ Formula
The coolest formula you probably never heard of!
This is the coolest formula that students are often NOT taught, but should be. It is based on a geometric analysis of x-intercepts, it always works, and is clean and simple.
Here’s the general idea. Solutions to a quadratic equation are a horizontal pair. That makes them equal distance from the line of symmetry, which travels vertically through the vertex.
So, to find the intercepts on just needs to find the midpoint, which is the x of the vertex, and the distance to the parabola from that midpoint.
The left-side intercept is M – D, the right-side is M + D. It’s clean, simple and easy!
If you’ve never seen this before, watch the video below.
Part 4: Completing the Square
Visually and Algebraically
Part 5: The Quadratic Formula
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
