Hello and welcome back to another week’s challenge problem. For those of you returning, thank you! I’m glad you’re here. It brings me a lot of joy knowing that other people enjoy doing math for fun! If you’re new, welcome.
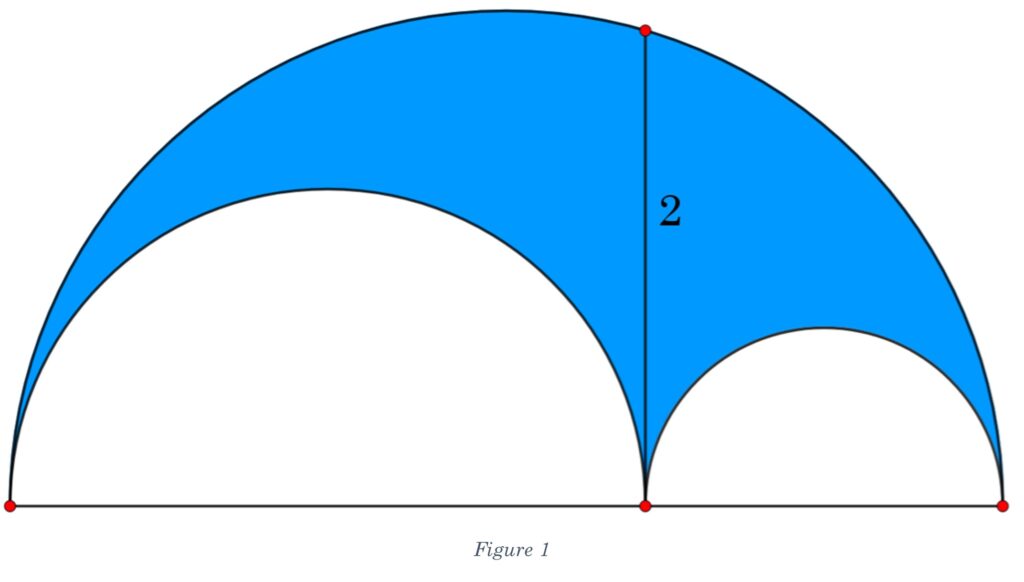
This week we are going to talk about three problems that share an answer. We will unpack how to find the area of the region shaded blue in the diagram at the top, but leave the others for you. You can find the three questions below.
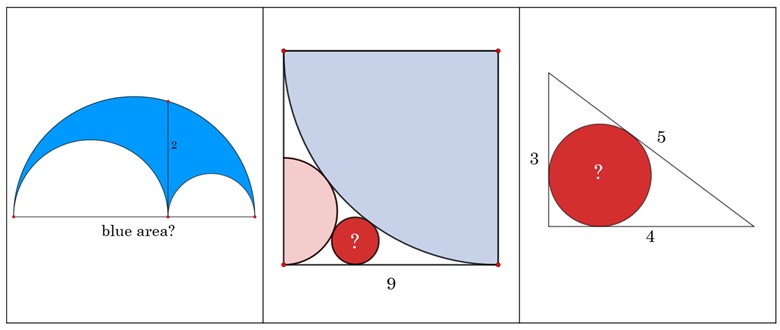
As is the tradition here, I will share three clues with you. Try the problem without the clue first, and come back to the clues should you get stuck.
The Details
The composite shape is comprised of three semicircles. The largest semicircle contains the other two, and the diameters of all three are co-linear. There is a line segment, length of 2 (units) that is tangent to the two smaller semicircles and has an endpoint on the diameter and edge of the larger semicircle.
I found this problem on a social media site. The author’s name is Aioub Sobhani.
Clue #1: The title of the article.
Clue #2: Deconstruct the composite shape and draw a pictograph of the formula you will use to find the area.
Clue #3: Express the diameter of the smaller semicircles in terms of the segment with length of two. Use the Pythagorean Theorem.
The Solution
How does the saying about eating an elephant go … one bite at a time? In that spirit, let’s deconstruct the shape into its components.
Imagine if the entire large semicircle was blue, then we added the two smaller semicircles in white on top of it. The area of the smaller semicircles would hide the blue area under them, leaving us with this strange shape, Figure 2.
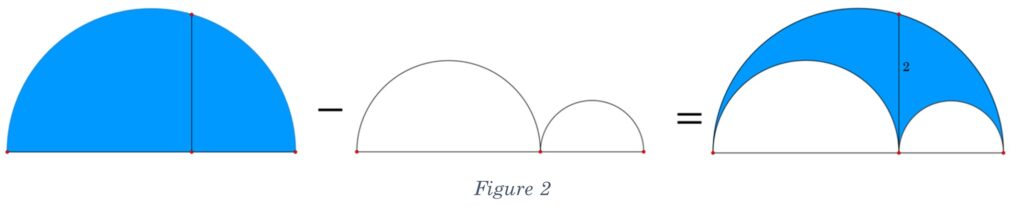
Our formula will then be the difference between the large semicircle and the sum of the two smaller semicircles. Before we formalize this with an algebraic expression, let’s talk about one of the best skills to use in these types of problems.
So often it happens that while creating names of points and names for things like radii or area, we end up with redundant information. In this case, one might want to label the diameter of each semicircle, creating three parameters. One of the best tricks in these problems is to express one thing in terms of another. Here we will label the diameter of each smaller semicircle and recognize that their sum is the diameter of the larger semicircle!

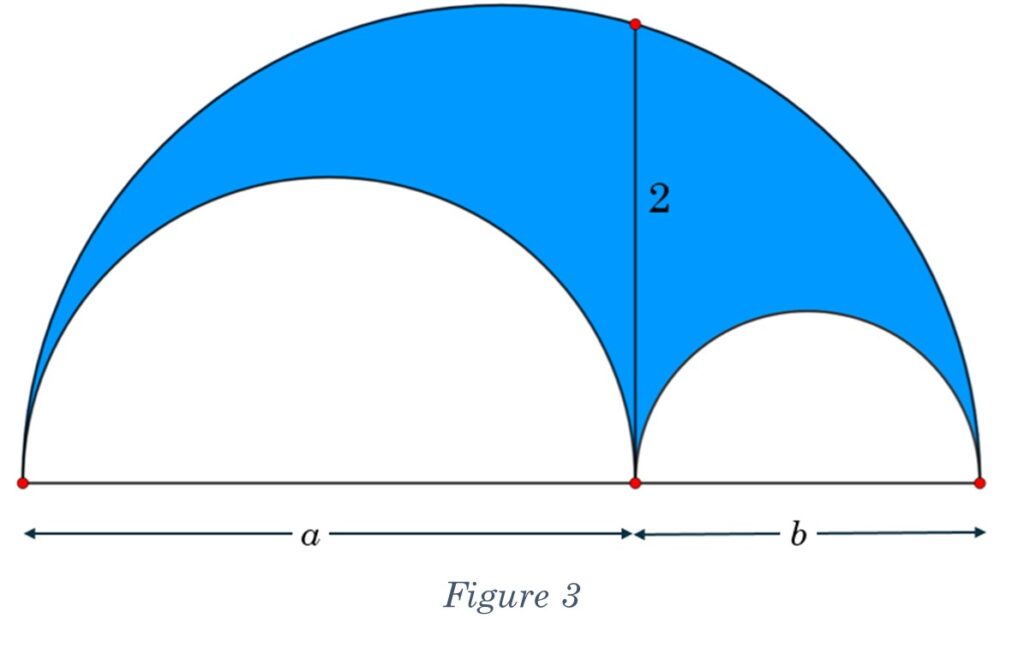
Let’s call the diameter of the larger circle a, and the diameter of the smaller circle b. That makes the diameter of the larger semicircle a + b.
You might be wondering, “Why are we labeling the diameter instead of the radius?” That’s an excellent question. For most circle explorations the radius is more useful. Here, however, it will prove cleaner to express the dimensions of the large and small circles in terms of the diameter than it would be for the radius.
The formula for the area of a circle is pi times the square of the radius, “pi r-squared.” We are dealing with semicircles, so we need to divide by 2. Since we are using the diameters instead of the radii, we will also need to divide those by 2.
Let’s define each part before putting them all together.

Simplification:
Like the emotions of a distraught teenager, this formula is messy and a bit all over the place. Let’s reel it in. To begin, we will factor out pi divided by two (Step 1). Then, we will square each term that squared (Step 2).
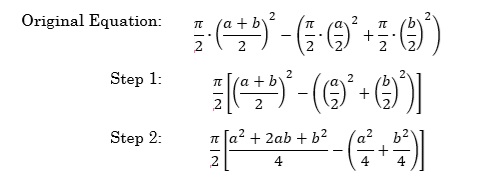
Inside of the brackets we have three terms, all fractions, and all with a denominator of four. Let’s clean that up, rewriting the entire thing as a single fraction. We will need to be cautious about the subtraction that is expressed because it is not just “a-squared divided by 4,” that’s being subtracted, but also “b-squared divided by 4.” We will see this in Step 3.
In Step 4 we will rearrange the terms so that the like terms will be located next to each other. Then, in Step 5, we will combine the like terms. In Step 6 we will reduce what remains inside of the brackets. Then, in Step 7, we will multiply by “pi divided by 2.”

What about ab?
Now for the infamous ab. Usually, these problems do not give information that is not required to find the solution. The line segment of length 2 is a clue that we will need to figure out how to use.
Like most of these problems, I had no idea how to use all of the clues. There are plenty of wrong turns, bad guesses, and surprising outcomes along the way. The path is unknown! In a video, or write-up like this, the meandering that occurs in problem solving is streamlined. But, rarely does someone just dive in and know exactly what to do ahead of time. If they did, the problem would not be much fun for them.
Let’s begin by creating a right-triangle from the end-point of the segment and the end points of a + b (Figure 4). The reason this is a right triangle is that any triangle that is (1) inscribed in a circle, and that (2) lies on the diameter contains a 90º angle. The 90º angle will have a vertex that is opposite of the diameter.
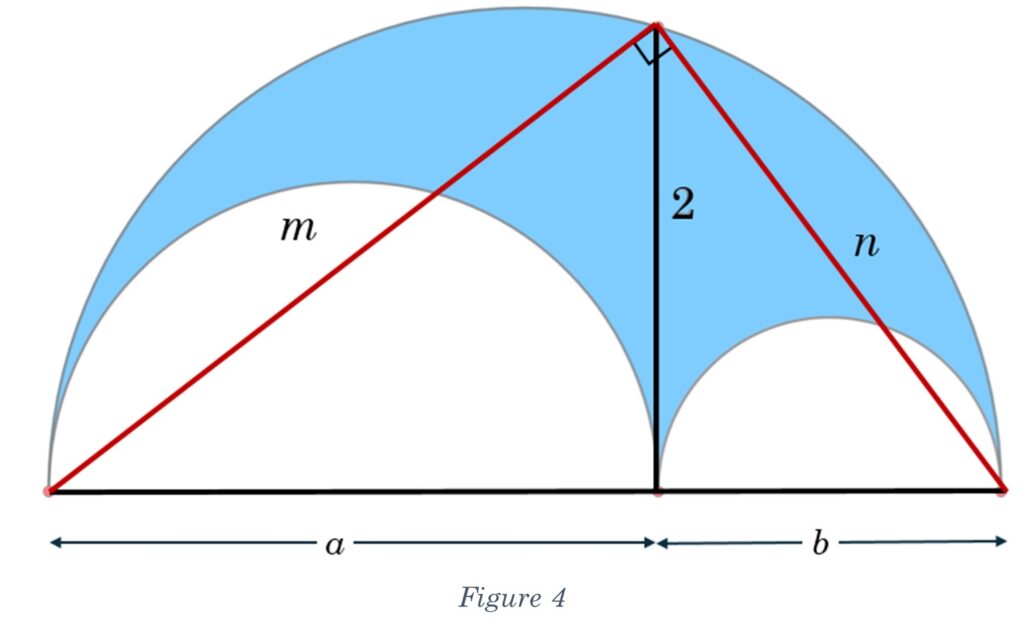
Our diagram has three right triangles. We know the segment of length 2 is perpendicular to the diameter because it is tangent to the smaller semicircles (that information was provided). A line tangent to a circle is perpendicular to the radius at the point of tangency. These two facts will not be unpacked and as it is assumed that the reader is familiar with high school Geometry. If not, you can just take it on faith that these assertions are true!
Our three triangles are as follows. One has a hypotenuse of a + b, and sides of m and n. One triangle has a hypotenuse m, and sides of a and 2. The last triangle has a hypotenuse we will call n, and sides of b and 2.
Now for the magic of hindsight. Let’s write out the Pythagorean Theorem for each of these triangles.

Do you see the substitution? We have an expression for m – squared and an expression for n – squared. Let’s substitute.
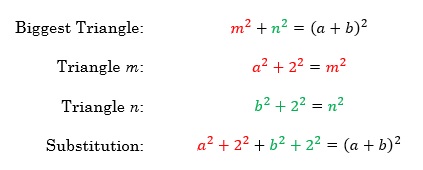
Next, we will combine like terms and square the right side of the equation.

Earlier we found that the area of the shape was pi times ab divided by four. We know ab is four. Plugging these values in and simplifying we find the following.
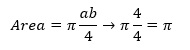
The area of the region shaded in blue is exactly pi. How cool is that?
What about the other two problems? I will not write up solutions to those as excellent solutions have been shared already by their authors (I assume they’re the authors of the problems, but maybe they are not). As you’ve undoubtedly guessed, the answer to each of those question is also pi. The fun is in discovering how that actually works.
The problem with the square with a side length of 9 has been done by Maths Paz. The link to his video can be found here. The right triangle with the inscribed circle was done by Andy Math. The link to his video can be found here. Both are excellent YouTube channels. Please check them out.
Wrap – Up:
How did you like this problem? Let me know, I’d love to hear from you!
If you are a math teacher and would like to use this problem I your classes, you can download the PowerPoint that I used to make the video solution, and that contains the images used in this article, right here.