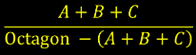
This math puzzle was a bit of a wild ride. The inspiration for the problem came from a YouTube video, linked here. I loved the problem and wondered how I could make some adaptations to the original. Hey, if six is good, eight is better, right?
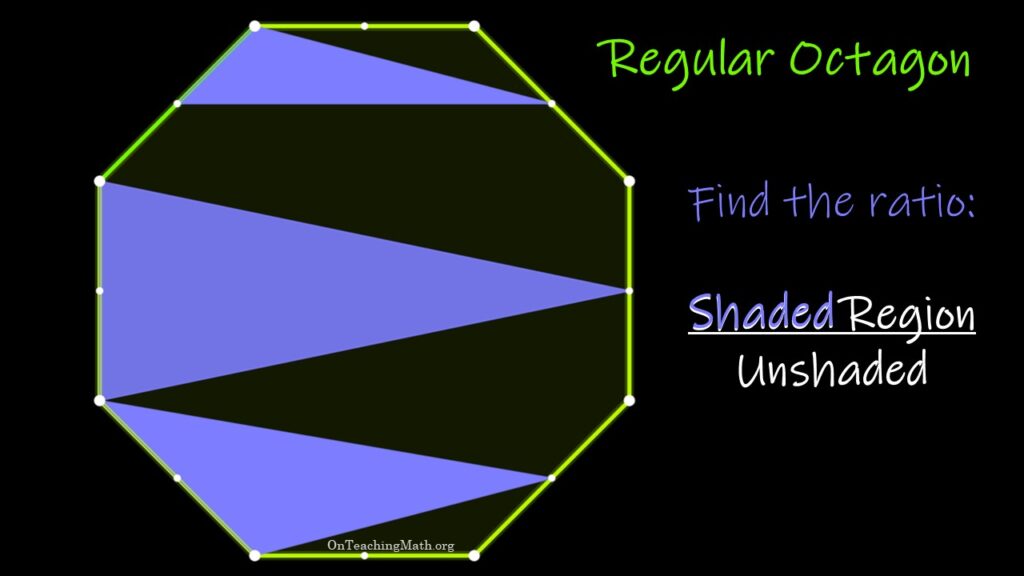
At 8:54 AM on a Saturday, I started the process with this octagon (Figure 1). I thought I solved the question of the ratio of the shaded:unshaded, and created a PowerPoint for a video of the problem.
About 2 PM I realized I had made a silly mistake and that I was wrong. Unfortunately, I had created all of the animations and diagrams, typed up all of the math, and was ready to record the video.
I reworked the problem only to realize the solution was not “pretty.” That wouldn’t do. One of the coolest things about these problems is that the solutions are simple, like 4:5 or just , or something like that.
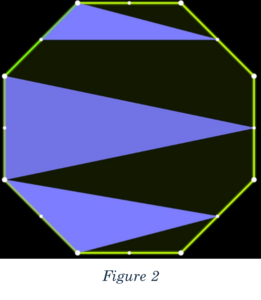
At 7:59 PM, I scrapped the problem and started over with the diagram shown in Figure 2.
However, I believe the result was worth the effort. I enjoyed this problem and think it worked out nicely.
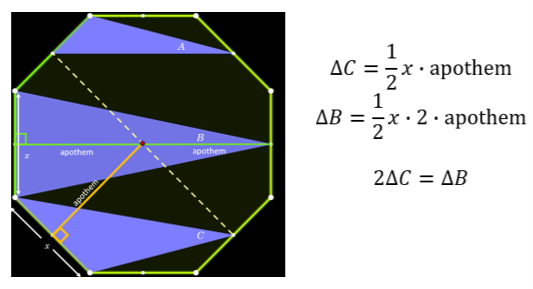
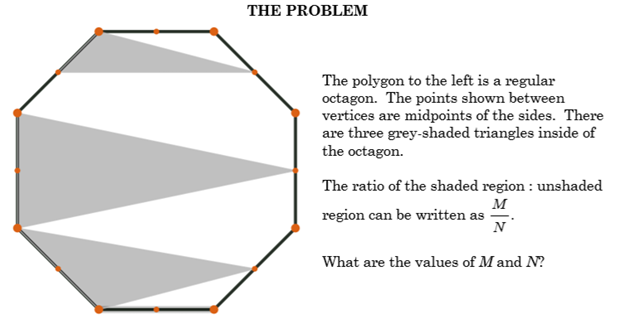
The question is, as mentioned at the beginning, what is the ratio of shaded:unshaded. The shaded is purple, the unshaded is black, the shape is a regular octagon and the midpoints of the sides are shown.
I’ll offer three clues, a link to the video solution, and then work through the solution here for you to read.
Are you ready? Try it out and see if you get it. If you get stuck, read clue #1.
Clue #1
At its essence, math is a language. It’s a written language, but so are many others. Languages are what we use to think! Thinking is a critical part of problem-solving.
So, clue #1 is to write out an equation or formula for the ratio (or fraction) of shaded to unshaded.
Clue #2
The features of regular polygons come into play, heavily, here. If you’re a little unfamiliar below you can see a diagram showing the important parts.
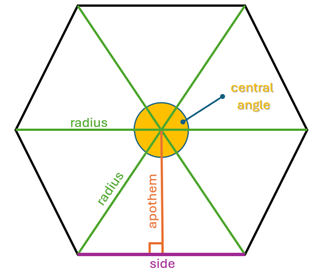
Combine these features with the fact that the areas that are shaded are all triangles and you’ll be on the right track.
Clue #3
What is the relationship between the sizes of each of these triangles? Write out each one and see if you can express the size of one compared to the other. This will help you simplify your equation and arrive at an “elegant,” solution.
Solution
You can see the video of the solution here.
Triangles Of course the area of a triangle is half of its base times the perpendicular height. That seems simple enough, but perpendicular height can be confusing and visually misleading.
The three triangles below all have the same area, even though the obtuse triangle might not look like it. This is because the perpendicular height is “outside,” of the triangle, so to speak.
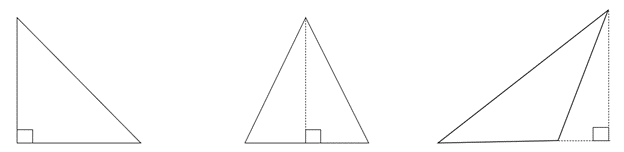
That’s the case with two of the three shaded triangles inside of our octagon. Sometimes seeing the height being perpendicular to the base is tricky, especially if the triangle is canted at an unusual angle.
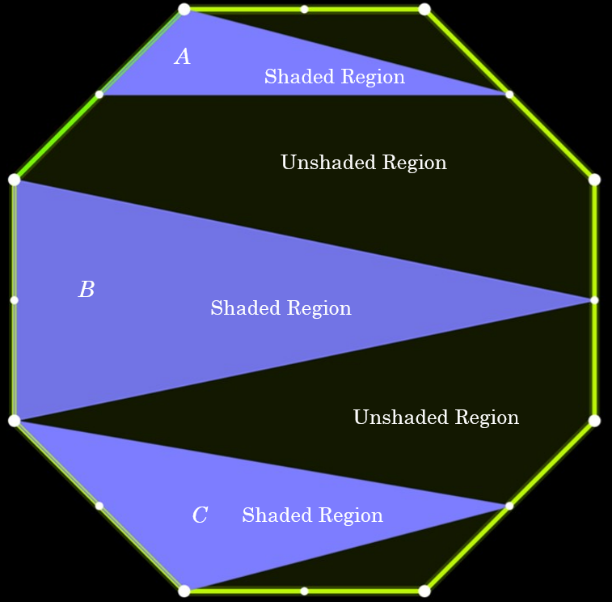
Let’s begin by defining our regions and coming up with a formula. Formulas help keep things organized, providing both a target and strategy for problem-solving.
The purple regions are shaded. Let’s call them triangles A, B, and C. The rest of the octagon is then the unshaded region. So, the unshaded region would be the triangles subtracted from the octagon.
Our job is to find the ratio of shaded to unshaded, which can then be expressed as the following.
Triangle B is isosceles because its base is the side of the regular octagon and the vertex opposite of the base is at the midpoint of the opposite side of the octagon from the base. That means that the height of the triangle is the distance from the midpoint of one side to the midpoint of the opposite side. This would pass through the center, making the height of triangle B twice the distance of the apothem.
Triangle C’s height is the apothem. You can see this clearly in the diagram below. Since triangle B’s height is double the height of triangle C, we can say that the area of triangle B is double that of triangle C. If we call the side length of the octagon x, we can write a formula for each triangle’s area.
Octagon’s Area:
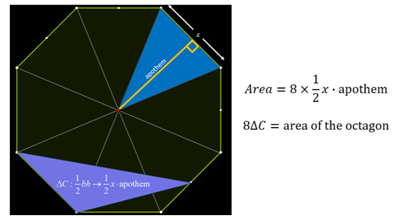
The area of the octagon is found by looking at one of the triangles that can be made from the central angle and a side. The base of such a triangle is the side, and the height is the perpendicular distance from that side (which we have called x), to the center of the octagon, the apothem.
That makes the area of the octagon eight times the area of triangle C.
The Last Triangle
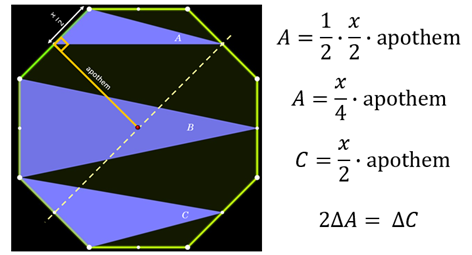
That leaves us to figure out triangle A. If we can express the size of triangle A in terms of triangle C, we will have the beautiful solution I hoped for.
As it turns out, the height of triangle A is also the apothem. Like triangle C, if you connect the midpoints of the sides adjacent to triangle A, you can see that the height of the triangle is the apothem. However, the base of triangle A is half of the side of the octagon, making it x divided by two. Triangle A and triangle C have the same height, but the base of triangle C is twice the size of triangle A.
Using the letters A, B, and C at this point to represent the area of the triangles, we can say the following.
2A = C
2C = B
2(2A) = B
4A = B
This allows us to rewrite A + B + C as A + 2A + 4A, which is 7A.
The octagon is 8C, and C = 2A. Therefore the octagon is 16A. Let’s plug all of that beauty into our original equation.

Now, how sweet is that?
You might be wondering, was it worth scrapping the original, ugly, problem in favor of this result? Yeah, I think so. I had a great time doing the problem. That makes it worth it.
I hope you enjoyed it. I very much appreciate you joining me on this process and hope you found this to be a beautiful problem as well!
Until next time,
Philip