If you’re a Douglas Adams fan, then you already know the answer. However, that doesn’t ruin the fun of this problem. When you try it, you’ll see why.
If you don’t know who Douglas Adams is, well, I suggest you buy a few books. There are a lot of TV and movie adaptations of his works, but the clever humor is almost entirely absent from those works. They’re good in their own rights but in a derivative sort of way.
As always, here’s how we will tackle the problem. I’ll give you a little background, and then share the details. The details will be followed by three clues, and then I’ll share my solution. At the end, I’ll share a link for teachers who would like to use this problem in their classrooms.
Background
While scrolling through social media I stumbled upon a hand-drawn version of this problem. I don’t mean to say it was done poorly, certainly not. The difficult part of writing such a problem is the sketch, but discovering the relationships between the features of the shapes or properties of the expressions that result in a pretty answer, like 7 or
I would love to give credit to the original author, but I don’t know who they are. There was a signature on the drawing, but it was written in what I believe is Hindi.
The Details
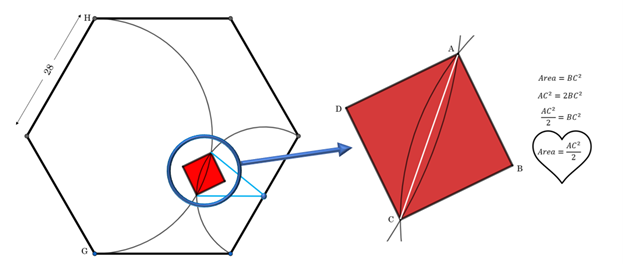
We have a regular hexagon with side lengths of 28 (units). There are two semicircles. The smaller of these intersects consecutive vertices of the hexagon. The large semicircle intersects the hexagon at points H and G, as shown in Figure 1.
The intersections of the semicircles create the diagonal length of a square. Our job is to find the area of the square.
If you’d like to try the problem on your own, now would be a good time to start because coming up next are the three clues. If you get stuck, read through one clue at a time and see if that gets you back on track.
Clue #1:
Instead of finding the side lengths of the square to find its area, look at the diagonal. How can you find the area of a square from knowing the diagonal?
Clue #2:
Create a sector in the small semicircle from the midpoint of the side to each end of the square’s diagonal. If you can find this angle, you can find the length of the diagonal.
Clue #3:
The interior angles of a regular hexagon are 120°. By connecting the vertices of the hexagon, and knowing that the side length is 28 (units), you can create a right triangle that shares the angle of the sector described in Clue #2.
The Solution
Watch a video of the solution here.
It was not entirely obvious to me that finding the diagonal of the square would be much easier than finding the side length. I spent a considerable amount of time before coming to this realization!
To express the side length of the square let’s look at the smaller of the two semicircles. The diameter of the semicircle is 28 (I’ll quit writing units every time, just know that the lengths are in units), making the radius 14. By connecting each end-point of the square’s diagonal to the semicircle’s center (each length being the radius), we create a sector whose segment is the diagonal of the square! It’s much easier to do than to write! See Figure 2.
You might be wondering where the formula, “AC squared divided by two equals the area,” comes from. Let’s unpack that here.
We can use the Pythagorean Theorem and the fact that a square’s sides are equal to find an expression for the square’s area from the length of the diagonal. That work is shown below in Figure 3.
Here is where writing up a solution is different than discovering a solution. Solving these types of problems for the first time is a bit like walking around in the dark in an unfamiliar house. We sometimes head for the bathroom only to find something useful in the kitchen by accident. Okay, that’s not my best metaphor, but, hopefully, you get the point. What you are about to read was not discovered in the neat sequence about to unfold. Only in hindsight is it possible to set this up in a step-by-step process.
Part 1
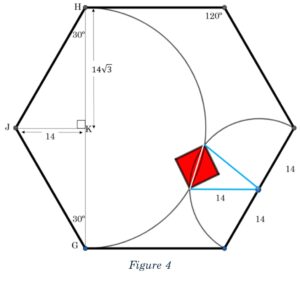
Create segment HG and label the vertex on the same side of the hexagon as H and G point J.
The perpendicular bisector of HG passes through J, creating two 30° – 60°– 90° triangles. The length of JH (side of the hexagon) is given as 28, making HK and GK both “14root3.” The length of JK will be just 14. You can see this in Figure 4.
Part 2
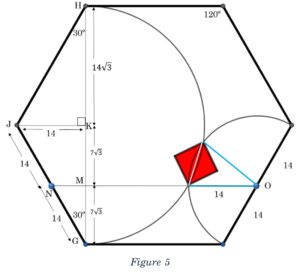
We will connect the midpoint of JG, which we will label N, to the center of the smaller semicircle, which we will call O. Because this is a regular hexagon this line will be perpendicular to HG and parallel to the “bottom” of the hexagon.
More importantly, line NO will coincide with one side of our sector!
Let us label the intersection of KG and NO point M. This creates another 30° – 60°– 90° right triangle that has a hypotenuse of 14. This tells us that MG is “7root3,” and MK will also be “7root3.” We could have discovered this fact from properties of a regular hexagon or similar triangles, but as the crude saying goes, there’s more than one way to skin a cat. I don’t know why that saying is a thing.
Part 3
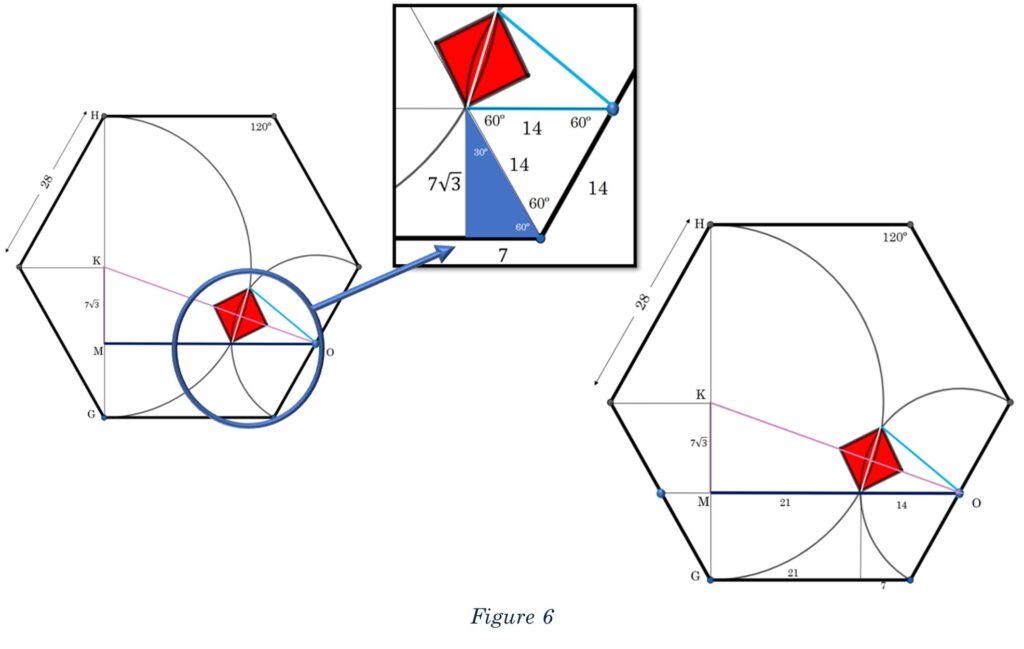
We’re almost to the biggest jump forward in this process, the point at which the path might become apparent. Let’s connect O to K creating a right triangle KOM.
It will turn out that angle KOM is half of the angle of our sector that we are looking for! Since we know KM is “7root3,” we just need one other side and we can use right-angle Trigonometry to find the angle KOM. Double that angle, and we’re almost home!
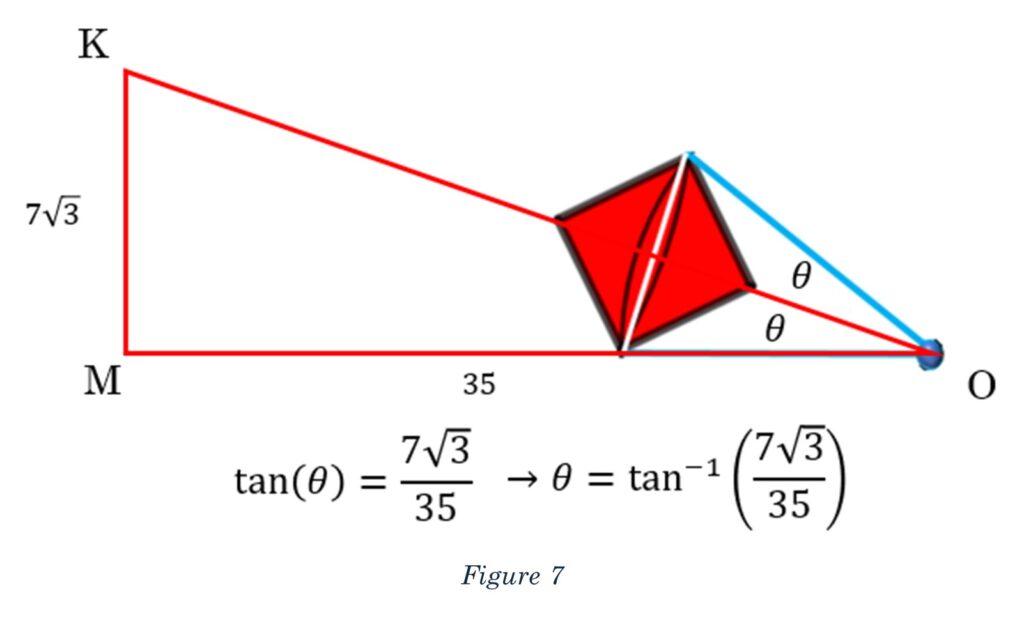
Let’s explore the length of segment MO. We know that from the end-point of the square’s diagonal to O is 14 because that’s the semicircle’s radius. But what about the rest of MO? We can create a segment from the hexagon’s bottom right vertex to the end-point of the square’s diagonal. This is an equilateral triangle. That segment bisects the interior angle of the hexagon, which can be seen if you extend this segment to the hexagon’s opposite vertex.
If we draw a line from the end-point of the square’s diagonal perpendicular to the “bottom,” of the hexagon, we will end up with yet another 30° – 60°– 90° right triangle. (I LOVE HEXAGONS!)
This allows us to find that the remaining distance of MO, after the semicircle’s radius, is 21, making MO have a length of 35. Let us revel in the exaltation brought forth by these wonderful 30° – 60°– 90° right triangles!
Part 4
In triangle KOM, we know side lengths KM and MO, which are perpendicular. This allows us to use tangent, as shown in Figure 7, where we find that angle KOM is “arctangent of 7root3 divided by 35.” For now, we will leave it as an exact value for later calculation.
Part 5
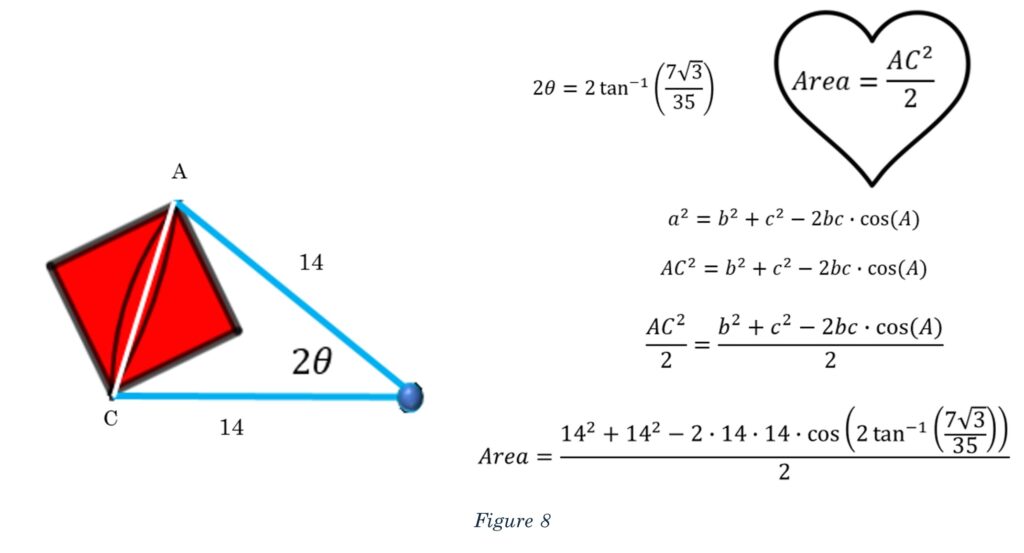
In Figure 8, we see a zoomed-in version of our square and sector. We can see that the sector angle is 2 and the side lengths are the radius, 14. We can use the cosine rule to find the length of the diagonal, which is labeled as AC. Once we have the length AC, we can square it and then divide it by 2 to find the area of the red square. The work is shown below.
The final calculation is left for you. It’s quite surprising that it turns out to be such a clean number. As is always the case, I do these problems over and over again, trying to make sure that mistakes aren’t made. Every time I did this calculation, with multiple calculators, I was surprised. It just doesn’t seem like 42 comes out of this.
In Closing
Douglas Adams wrote, among other great books, shows, and skits, The Hitchhiker’s Guide to the Galaxy. There are TV and movie adaptations to this book, which didn’t originally start off as a book but grew into one. Those adaptations are good, but the mathematically clever humor in the book is almost entirely lost in those TV episodes and the movie.
Without trying to give away why the quote is funny, but allowing the unfamiliar with Adams access to the title of this problem, let me explain. The famous quote from Hitchhiker’s Guide to the Galaxy is,
“The ultimate answer to life, the universe and everything is … 42!”
If you have not read any of Douglas Adams’ work, I’d highly recommend it.
I hope you enjoyed this problem. I found it very entertaining. I created the diagram in GeoGebra and printed it off. Then, with a straight edge and pencil, I began drawing all sorts of things on the hexagon and finding various parameters and measurements. It took me a bit to stumble upon the solution’s path as I started off trying to find the side length of the square.
That’s the joy of these questions, discovering that little surprise, which is often looking at the same thing in a new way that makes everything fall into place.
If you’re a math teacher and would like to use this problem in your classroom, the links below contain a student handout and PowerPoint. Feel free to use them with your students!
Thank you again for reading. Until next week, vaya con dios, as they say in the old Westerns.
