A Refresher ... if you need.
Before we dive in, if you’re unfamiliar with Voronoi Diagrams, perhaps this short video will get you firmly grounded with the basics. This problem does not involve complex applications of Voronoi Diagram concepts, so a little teaser is all you should need.
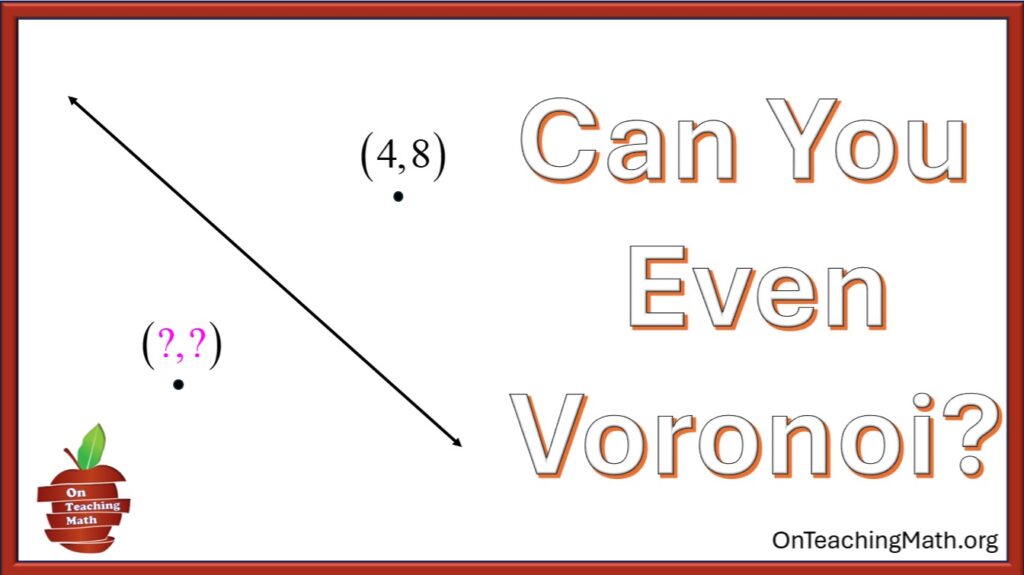
What this problem demands is for you to find the coordinate of the missing cell-point, as shown in the diagram above.
Clues
The boundary line separating adjacent cells is the perpendicular bisector to the segment connecting adjacent cells’ cell points. In our case, that would be connecting (4, 8) to our unknown coordinate.
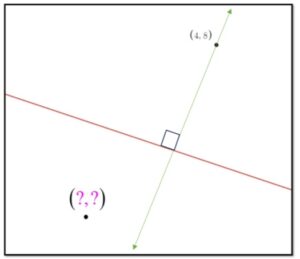
The intersection of the boundary line and the segment connecting (4, 8) to the unknown point is the midpoint of the ends of the segment (4, 8) and (?, ?). To find the midpoint you can set the lines equal and solve for x, then find y, or you can use a graphing calculator.
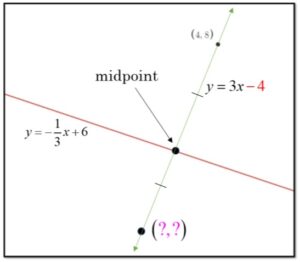
Use the midpoint formula to find the missing values of x and y.
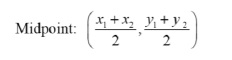
Solution Walk-Through
The video to the right will walk you through the process described below.
Equation of the Segment
We know that our unknown point and (4, 8) are on a segment that is perpendicular to, and bisected by, the boundary line given. So, to begin we will discover the line of the segment connecting (4, 8) and the unknown point. Let’s begin with the slope, which will be 3 as that is the negative reciprocal of the slope of the boundary line.
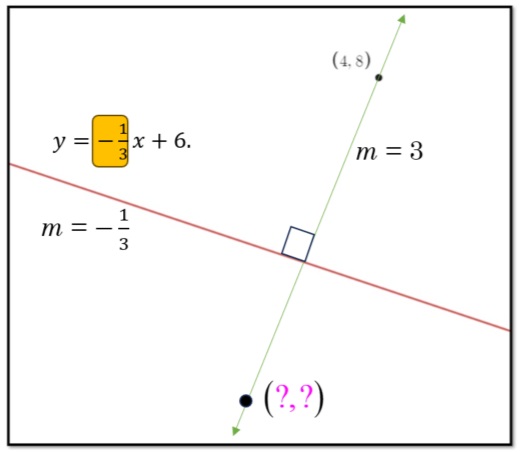
Knowing the slope is 3, and it passes through the point (4, 8), let’s plug those values into y = mx + b, to find the equation of the line.
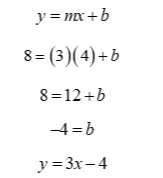
The equation of the segment connecting (4, 8) and the unknown coordinate is y = 3x – 4. Nice!
The Midpoint
Where the boundary and our segment intersect is the midpoint of the segment. That will allow us to find the missing coordinate. To find the midpoint we will set the lines equal and solve for x. This is the x – coordinate of the midpoint. We can plug this value into either equation to find the y – coordinate.
We have found that the midpoint is at (3, 5).
Using the Midpoint to Find (?, ?)
We will write the midpoint formula, plug in the values (4, 8) for x1 and y1, and then (3, 5) as the midpoint, and then solve for the unknown values.

Resources and Reflections
First off, this is a great topic to teach students that are past Algebra 1 level, but need some work on linear equations (so pretty much all students past Algebra 1). It is a fresh way to practice slope, writing equations, solving linear equations, using formulas, and all of that good old linear equations stuff.
If you would like to use this problem as either a lesson or a challenge problem, you can grab a copy of the PowerPoint, student handout, and Google Forms quiz containing and supporting this very problem. Click here to download your copy.
If you like this kind of content and would like to receive a weekly problem in your email, please consider signing up for our Substack.
What Do the Free Resources Look Like?
To the right you can see a screen shot preview of what the assignment looks like in Google Forms. Students are given chances to refresh their memories and learn, or to see up to three clues before trying the question.
When they submit the question they get immediate feedback and a video explaining the solution.
You can post this in Google Classroom and use it however you see best!
Below you can see what the student hand-out or flier looks like. Notice that there are two QR codes that students can use.
In addition to these resources you will also receive an animated PowerPoint, pretty much the same PowerPoint that was used to make the video of the solution.