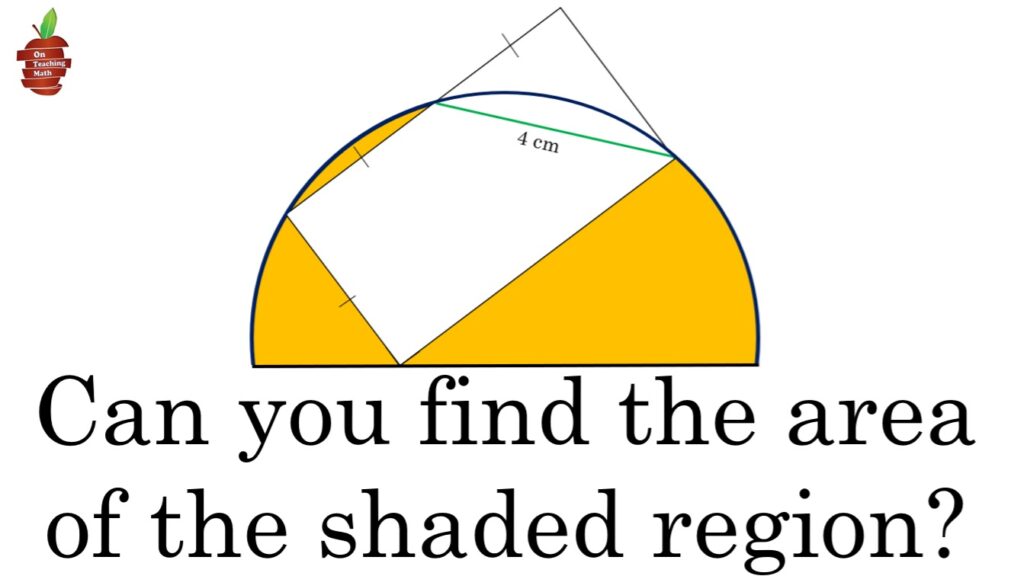
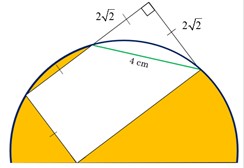
Here are the details: We have a semi-circle with a chord length of 4 cm, and a rectangle with a width that is twice the height, as shown in the diagram.
Our job is to find the area of the shaded (yellow) region.
Use the clues below if you’d like to try this for yourself before jumping into the solution.
Clues
Clue #1: Find the width of the rectangle. There’s an isosceles right triangle with a hypotenuse of 4 cm.
Clue #2: If the triangle is isosceles, each angle is 45 degrees. What’s the collinear angle’s measure? If you complete the circle, look at the arc that is intercepted by the collinear angle. Is the collinear angle inscribed or central?
Solution
Making Sense of the Shape
To begin let’s define what the shaded area is, or rather, what it is not. The shaded area is most of a semi-circle, but there are two pieces missing. The first missing part is the trapezoid (the rectangle cut by the chord in the circle). The second missing part is a segment.
This means that the shaded area is a semi-circle minus the trapezoid and also minus the segment. The formulas for each of these components is shown below.
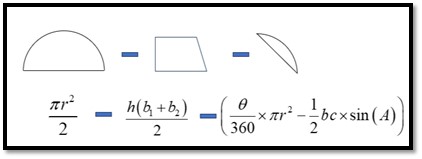
The area of the segment is a bit tricky. Below you can see how the segment is a sector (like a pizza slice), with the end cut off. The segment is the sector minus the triangle.
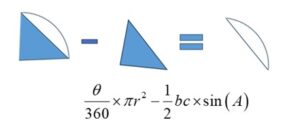
It is not initially obvious that the area of the triangle will require the sine formula for the area of a triangle, but as we get to that part, you will see that it is the case.
In order to use the formula for the shaded area we will need to find the radius, the parts of the trapezoid, and the angle of the sector (which makes the segment). Let’s make a list.
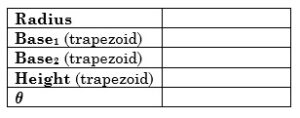
The Rectangle
Let’s begin with figuring out the rectangle.
The chord length is 4 cm. The rectangle has a 90 degree angle, and the height is half of the width. Using the Pythagorean theorem we can find that each side is “2root2”.
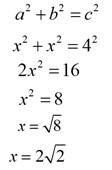
Now we know the height of the trapezoid is “2root2,” and the width is twice that, “4root2.”
The Radius
The radius is the most difficult thing to find since we don’t know how to find the center of the circle. There are clues, but they’re rather obscure. There are two key facts we must recall to find the radius.
- An inscribed angle’s measure is half the measure of the subtended arc.
- A central angle’s measure is the same as the subtended arc.
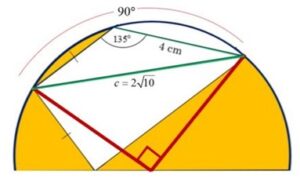
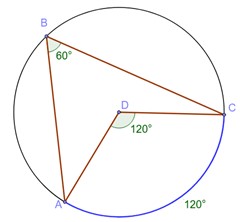
Earlier we established that we had a 45-degree angle. The collinear angle is then 135-degrees, which makes its intercepting arc 270-degrees. That leaves 90-degrees left from which we can construct a central angle that is 90-degrees.
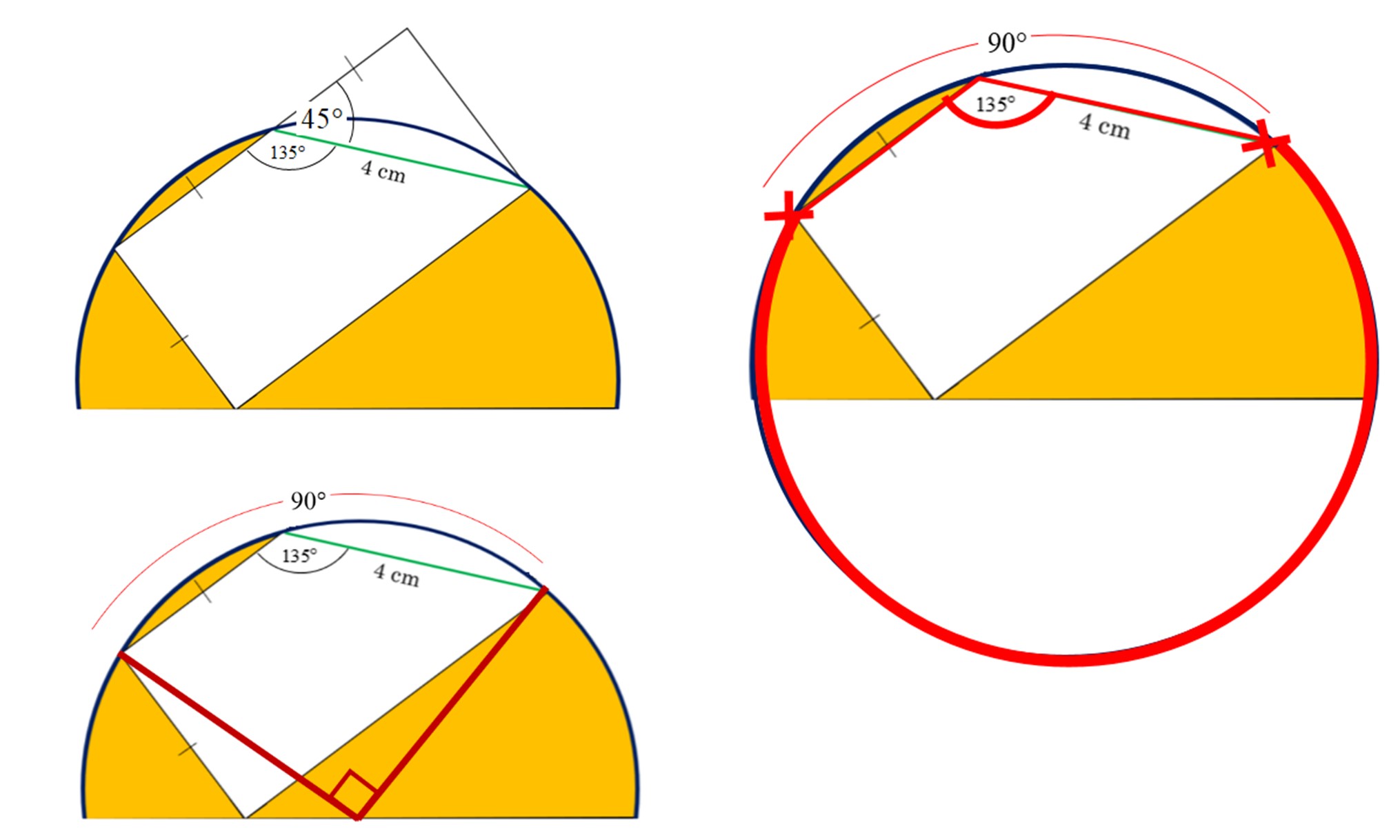
In the last diagram you can see a quadrilateral. If we split that quadrilateral into two triangles, the “top,” triangle with the circle’s chord in green (4 cm) has two known angles and the included angle. This is ripe for the picking, should we decide to use the cosine rule.
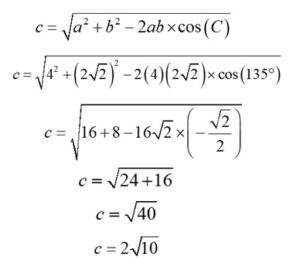
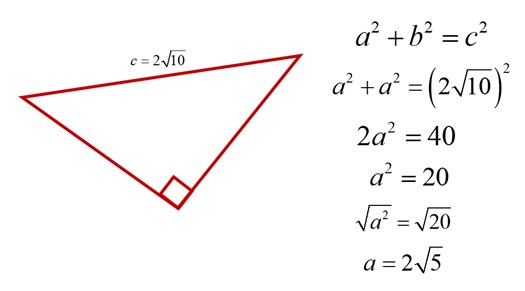
Now we know the hypotenuse of the right triangle in red is “2root10.” We can use the Pythagorean theorem again to find the legs, which are also the radius!
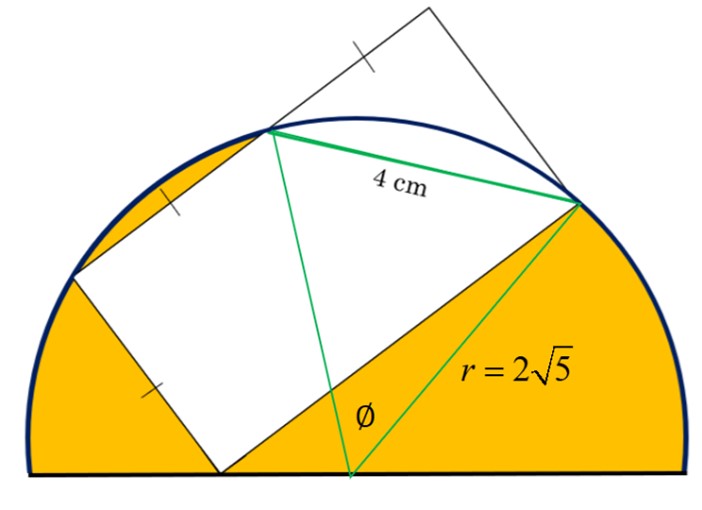
One last thing, and it’s a bit tricky, but not as hidden as the radius. We need to find the sector’s angle. Let’s take a look at a diagram clearly showing what we are dealing with.
For this triangle we know all three sides, but need to know the angle. This is a different application of the cosine rule! How cool!
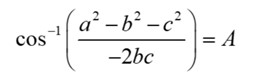
Here both sides b and side c are “2root5,” and side a is 4. A little calculator computer will show us that the angle θ = 53.1 degrees, rounded to three significant figures.
Let’s collect our information in the table below.
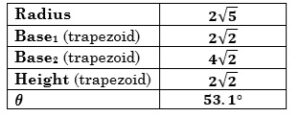
For the Calculation
Now it’s time for a Michael Scott comment for the mathematical approach called plug and chug. We will enter all of these values into the formula and do some computation. Note, it’s best to simplify as much as is easily before plugging the values into a calculator. People make more mistakes from using the calculator than they do from doing simple arithmetic on paper.
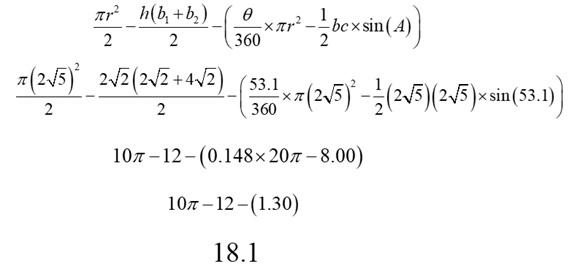
Let’s see if that makes sense. The area of the semi-circle would be Taking away the trapezoid, which is 12 square units, leaves us at just over 19 square units. Take away the little sliver … seems reasonable to me. What are your thoughts?
Post a physical copy of the problem in your room, preferably in a place reserved for weekly Challenge Problems. Upload the Google Forms version of the problem in Google Classroom and then wait for a week.
When it’s all done, use the PowerPoint in class as a Socratic Lesson. Be the guide and let students push the problem-solving approaches.
This problem has heavy doses of Geometry and Trigonometry. Students will need to use arcs, inscribed and central angles, sectors and circle segments, the cosine rule and the sine formula for the area of a triangle, along with general equation writing skills! It’s a bit of a monster. Can you solve it? Give it a shot.
Use This in Your Classroom
Click the thumbnail to the left to download the PDF file that links all of the resources included here.
You’ll find a PowerPoint (not compatible with Google Slides because of the animation and layering), a print-out for students, and a link that will have you create your copy of the Google Forms “quiz,” in your Google Drive.
The Google Forms “quiz,” is set up to allow students to get clues and help as they work on the problem. They can answer the question whenever they’re confident.
If you like this type of resource, please search our site for other challenge problems as well as lessons, quizzes, student hand-outs, and so on. Our goal is to create one challenge-problem a week for every week in 2024. Each problem will have a student hand-out, solution video, PowerPoint lesson, and Google Forms Quiz. So, stay tuned!
