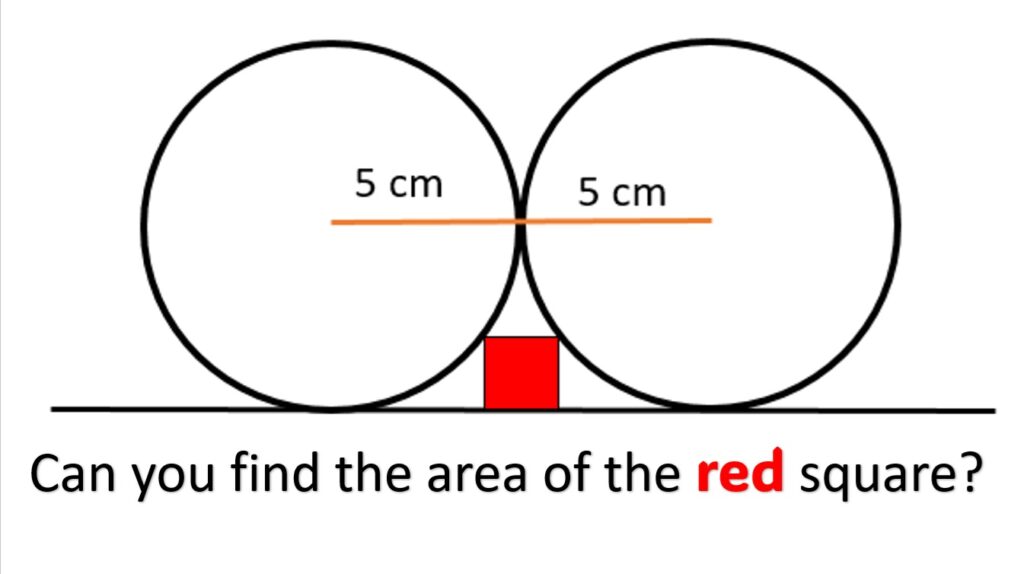
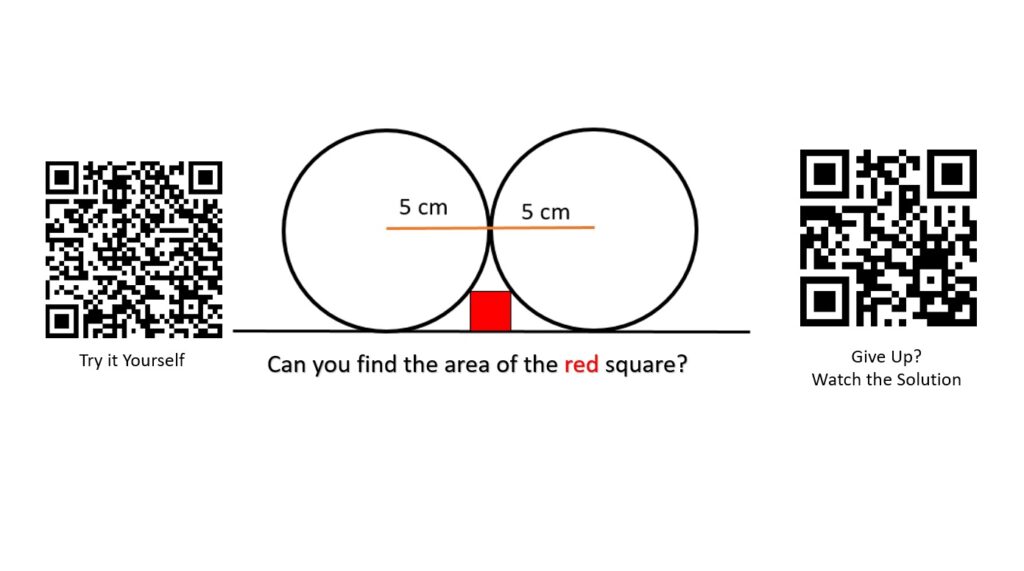
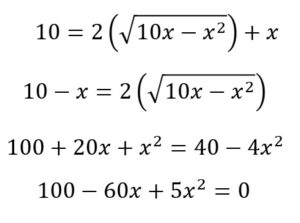Here are the details: We have two identical circles, both with a radius of 5 cm. They’re both tangent to the same line and share one point in common, as seen in the diagram above. There’s a beautiful little red square sandwiched between the circles. The square has a vertex on the edge of each circle and the opposite side from those vertices coincides with the tangent line.
What is the area of the square?
Clues
Clue #1: Can you express the radius of the circle in terms of the height of the square?
Clue #2: You can use the Pythagorean Theorem with a right triangle from the center of one circle to the vertex of the square to write an expression for the square’s height.
Clue #3: The height of the square plus twice this length found in Clue #2 equals 10 cm.
Watch the video to see the solution.
Solution
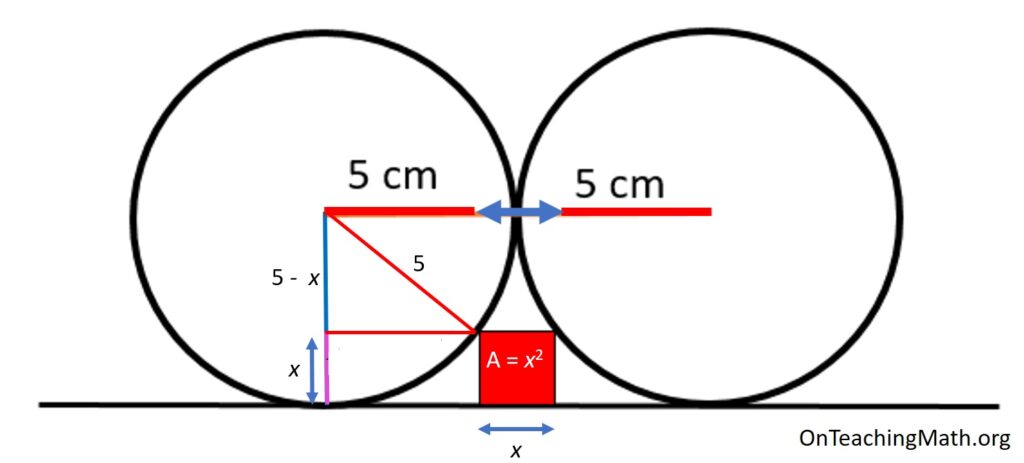
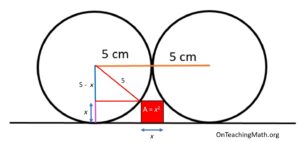By connecting the circle’s center to the vertex of the square we can create a right triangle.
Let’s call the height of the square x. Since the radius of the circle is 5 cm, the hypotenuse of our triangle is 5 cm. One leg will be 5 – x, since 5 is the radius and x is the height of the square.
All of this works because the line is tangent to the circle, making the line from the point of tangency perpendicular to radius. Since the square coincides with the tangent line, we know things are all parallel where they should be (in the vertical direction) and perfectly perpendicular to the horizontal direction.
We can use the Pythagorean Theorem to find the missing side of the triangle.
Here’s the coolest part. The two radii combine to make a 10 cm line. We know that 2b + x = 10 cm.
This gives the equation shown below.
This quadratic equation is factorable, producing two real number results, 10 and 2. Since the side of the square is smaller than the radius (5 cm), we can throw out the answer of 10. The side length of the square is 2 cm.
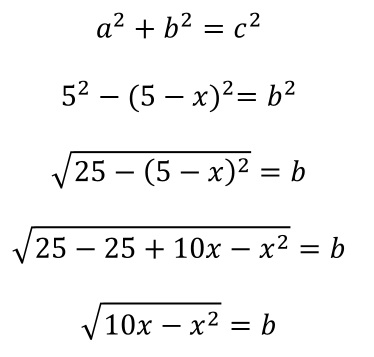
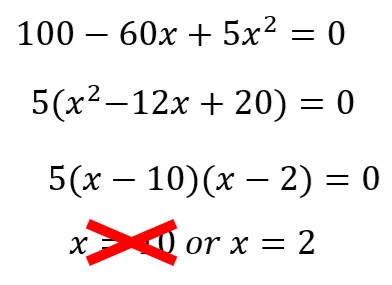
The beautiful little red square has an area of 4 square centimeters! How cool is that?
How did you like this problem? Did you get the same answer? Let me know if you found it with a different method!
Download a Copy of the Student Handout
Below you will find two buttons. One allows you to try the Google Forms quiz version of this question as a student would. The other allows you to copy a version of the Google Form to your Google Drive. This way you can use it in your classroom.
